có bao nhiêu số tự nhiên có bốn chữ số trong đó có đúng hai chữ số 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



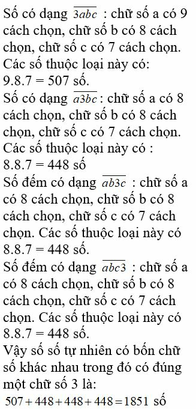
Số có dạng 3 a b c : chữ số a có 9 cách chọn, chữ số b có 8 cách chọn, chữ số c có 7 cách chọn. Các số thuộc loại này có: 9.8.7 = 507 số.
Số có dạng a 3 b c : chữ số a có 8 cách chọn, chữ số b có 8 cách chọn, chữ số c có 7 cách chọn. Các số thuộc loại này có : 8.8.7 = 448 số
Số đếm có dạng a b 3 c : chữ số a có 8 cách chọn, chữ số b có 8 cách chọn, chữ số c có 7 cách chọn. Các số thuộc loại này có 8.8.7 = 448 số.
Số đếm có dạng a b c 3 : chữ số a có 8 cách chọn, chữ số b có 8 cách chọn, chữ số c có 7 cách chọn. Các số thuộc loại này có 8.8.7 = 448 số.
Vậy số số tự nhiên có bốn chữ số khác nhau trong đó có đúng một chữ số 3 là: 507 + 448 + 448 +448 = 1851 số
Nhận xét: Bài toán yêu cầu có duy nhất (đúng một) số 3, các chữ số chỉ lặp lại có đúng 1 lần vì vậy khi giải toán cần đọc kỹ yêu cầu đề toán.



Các số đó là:
-Số các số có đúng 2 chữ số 3 ở cuối :1033;1133;1233;...;9933 là: 99-10+1=90 số
-Số các số có dạng a33b :1330;1331;1332;...;9339 là : 99-10+1=90 số
-Số các số có dạng a3b3 :1303;1313;1323;....;9393 là :99-10+1=90 số
-Số các số có dạng 3a3b :3130;3132;3133;....;3939 là :99-10+1=90 số
-Số các số có dạng 33ab :3310;3311;3312;...;3399 là :99-10+1=90 số
Vậy có tất cả 90+90+90+90+90=450 số có đúng 2 chữ số 3.
Lúc đầu đọc bạn sẽ không hiểu nếu nghiên cứu dần dần bạn sẽ hiểu ngay thôi ^^ nha