CHo \(\widehat{xOy}\)và \(\widehat{yOz}\)là 2 góc kề bù. Om là tia phân giác của \(\widehat{xOy}\); On là tia phân giác của \(\widehat{yOz}\). Tính \(\widehat{mOn}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 9 2023
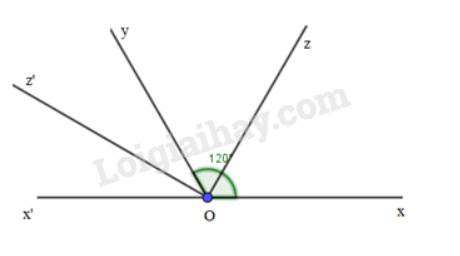
Vì Oz là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.120^\circ = 60^\circ \)
Vì Oz’ là tia phân giác của \(\widehat {yOx'}\) nên \(\widehat {x'Oz'} = \widehat {yOz'} = \frac{1}{2}.\widehat {yOx'} = \frac{1}{2}.60^\circ = 30^\circ \)
Vì tia Oy nằm trong \(\widehat {zOz'}\) nên \(\widehat {zOz'}=\widehat {zOy} + \widehat {yOz'} = 60^\circ + 30^\circ = 90^\circ \)
Vậy \(\widehat {zOy} = 60^\circ ,\widehat {yOz'} = 30^\circ ,\widehat {zOz'} = 90^\circ \)
Chú ý:
2 tia phân giác của 2 góc kề bù thì vuông góc với nhau
27 tháng 7 2017
Bài 2:
\(a.\)Vì \(\widehat{xOy}\)kề bù với góc \(\widehat{yOz}\)\(\Rightarrow\)\(\widehat{xOy}+\widehat{yOz}=180^0\)
\(\Rightarrow\) \(60^0+\widehat{yOz}=180^0\)
\(\Rightarrow\) \(\widehat{yOz}=180^0-60^0=120^0\)
\(b.\) Vì \(Ot\)là tia phân giác \(\widehat{xOy}\)\(\Rightarrow\)\(\widehat{tOy}=\frac{\widehat{xOy}}{2}=\frac{60^0}{2}=30^0\)
Vì \(Om\)là tia phân giác \(\widehat{yOz}\)\(\Rightarrow\)\(\widehat{yOm}=\frac{\widehat{yOz}}{2}=\frac{120^0}{2}=60^0\)
Vì \(Oy\)nằm giữa 2 tia \(Ot\)và \(Om\) \(\Rightarrow\) \(\widehat{tOy}+\widehat{yOm}=\widehat{tOm}\)
\(\Rightarrow\) \(30^0+60^0=\widehat{tOm}\)
\(\Rightarrow\) \(90^0=\widehat{tOm}\)
Vậy \(\widehat{tOm}\)là góc vuông
27 tháng 7 2017
Bài 2: Vì góc xOy và yoz kề bù nên góc xOz= 180 độ Ta có : Góc xoy + góc yoz = xOz Hay : 60 độ + góc yoz = 180 độ góc yoz = 180 độ - 60 độ = 120 độ Vậy....
H
22 tháng 4 2019
Cái này mình bt làm nek
Vì Om là tia phân giác của\(\widehat{xOy}\)
\(\Rightarrow\widehat{xOm}=\widehat{mOy}=\frac{\widehat{xoy}}{2}\)
Vì On là tia phân giác của \(\widehat{yOz}\)
\(\Rightarrow\widehat{zOn}=\widehat{yOn}=\frac{\widehat{yOz}}{2}\)
Vì Oy nằm giữa On và Om
Nên\(\widehat{mOy}+\widehat{nOy}=\widehat{mOn}=\frac{\widehat{xOz}}{2}\)
Hay\(\frac{\widehat{xOy}}{2}+\frac{\widehat{yOz}}{2}=\frac{\widehat{xOz}}{2}\)
\(\Rightarrow\widehat{mOn}=\frac{180^o}{2}=90^o\)
22 tháng 4 2019
vì góc xOy và yOz là 2 góc kề bù
\(\Rightarrow xoy+yoz=180\)
tia om là tiaphaan giác của góc xoy
\(\Rightarrow moy=mox=xoy:2\)
tia on là tia phân giác của góc yoz
\(\Rightarrow noy=noz=yoz:2\)
\(\downarrow\)
noy:2+moy:2=180
TH
9 tháng 3 2017
vì góc xOz là góc kề bù=>góc xOz=180 do
=>Tia Oy nằm giữa 2 tia Ox; Oz
Vì tia Oy nằm giữa 2 tia Ox; Oz=>xOy+yOz=xOz
Thay xOy=60do;xOz=180do
60+yOz=180
yOz=180-60
yOz=60
HT
1 tháng 7 2019
a) Ta có \(\widehat{xOy}\) và \(\widehat{yOz}\) là 2 góc kề bù (theo đề)
\(\Rightarrow\widehat{xOy}+\widehat{yOz}=180^0\)
Hay \(50^0+\widehat{yOz}=180^0\)
\(\Rightarrow\widehat{yOz}=130^0\)
b) Góc mOn ..... bn tự lm ik
Ta có: Om là tia phân giác của \(\widehat{xOy}\) (theo đề)
\(\Rightarrow\)\(\widehat{xOm}=\widehat{yOm}=\frac{\widehat{xOy}}{2}=\frac{50^0}{2}=25^0\)
Lại có : On là tia phân giác của \(\widehat{yOz}\) (theo đề)
\(\Rightarrow\)\(\widehat{yOn}=\widehat{zOn}=\frac{\widehat{yOz}}{2}=\frac{130^0}{2}=65^0\)
Ta lại có: \(\widehat{mOy} + \widehat{nOy} = 25^0 + 65^0 = 90^0\)
Do đó 2 góc mOy và nOy phụ nhau.
KT
10 tháng 8 2018
Om là phân giác góc xOy
=> góc mOy = 1/2 góc xOy
On là phân giác góc yOz
=> góc yOn = 1/2 góc yoz
suy ra: góc mOy + góc yOn = 1/2 (góc xOy + góc yOz)
<=> góc mOn = 1/2.1800 = 900 (do góc xOy và góc yOz kề bù)
10 tháng 8 2018
Om phân giác xoy => moy=1/2xoy hay xoy=2moy
tương tự => noy=1/2yoz hay yoz=2noy
Lại có:
xoy+yoz=180
=>2moy +2noy=180
=>moy+noy=90 hay mon =90
giúp !