một số có 2 chữ số .biết rằng chữ số hàng đơn vị gấp 3 lần chữ số hàng chục .nếu đổi chỗ 2 chữ số cho nhau ta được số mới lớn hơn số cũ 54 đơb vị .tìm số ban đầu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 8 2019
Gọi số cần tìm là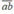 
= 10a + b (a, b ∈ N. 0 < a < b < 10)
Ta có b = 3a
Khi đổi hai chữ số ta được số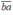 
= 10b + a
Vì số mới lớn hơn số cũ 54 đơn vị nên ta có phương trình: 10b + a – 54 = 10a + b
⇔ 9b – 9a = 54
⇔ 9.3a – 9a = 54
⇔ 18a = 54
⇔ a =3 (tmđk)
Vậy số ban đầu cần tìm là 39.
23 tháng 4 2021
Ta có các số tự nhiên có 2 chữ số mà chữ só hàng đơn vị gấp ba lần chữ số hàng chục là 39;26;13
ta lần lượt thử các số
viết ngược của 13 là 31, lớn hơn số ban đầu : 31-13=18 (loại)
viết ngược của 26 là 62, lớn hơn số ban đầu :62-26=36 (loại)
viết ngược của 39 là 93, lớn hơn số ban đầu :93-39=54 (thỏa mãn)
Vậy số cần tìm là 39
TH
27 tháng 7 2017
= > Ta có các số : 31 ; 62 ; 93
Mà : 31 - 13 = 18 ( loại )
62 - 26 = 26 ( chọn )
93 - 39 = 54 ( loại )
Vậy = > Số đó là : 62
PA
25 tháng 7 2019
Đáp số: 45
\(4\times2=8\)
\(8-5=3\)
Đổi chỗ 2 số ta được 54 lớn hơn 45 là 9 đơn vị.
Học tốt (◠‿◠)
BB
6 tháng 2 2020
Số đó có dạng: ab và ba
ab - ba = 54
Hàng chục gấp 3 lần hàng đơn vị -> số đó là 31, 62, 93
31 - 13 = 18 ( loại )
62 - 26 = 36 ( loại )
93 - 39 = 54 ( lấy )
Vậy số là 54
Nhớ k cho mk nhé
Gọi số cần tìm là \(ab\left(ab\in N.0< a< b< 10\right)\)
Ta có : \(b=3a\)
Khi đổi hai chữ số ta được số \(ba=10b+a\)
Vì số mới lớn hơn số cũ 54 đơn vị nên ta có phương trình:
\(10b+a-54=10a+b\)
\(\Leftrightarrow9b-9a=54\)
\(\Leftrightarrow9.3a-9a=54\)
\(\Leftrightarrow18a=54\)
\(\Leftrightarrow a=3\left(tm\right)\)
Mà \(b=3a\) nên \(b=3\times3=9\left(tm\right)\)
Vậy số cần tìm là \(39\)