
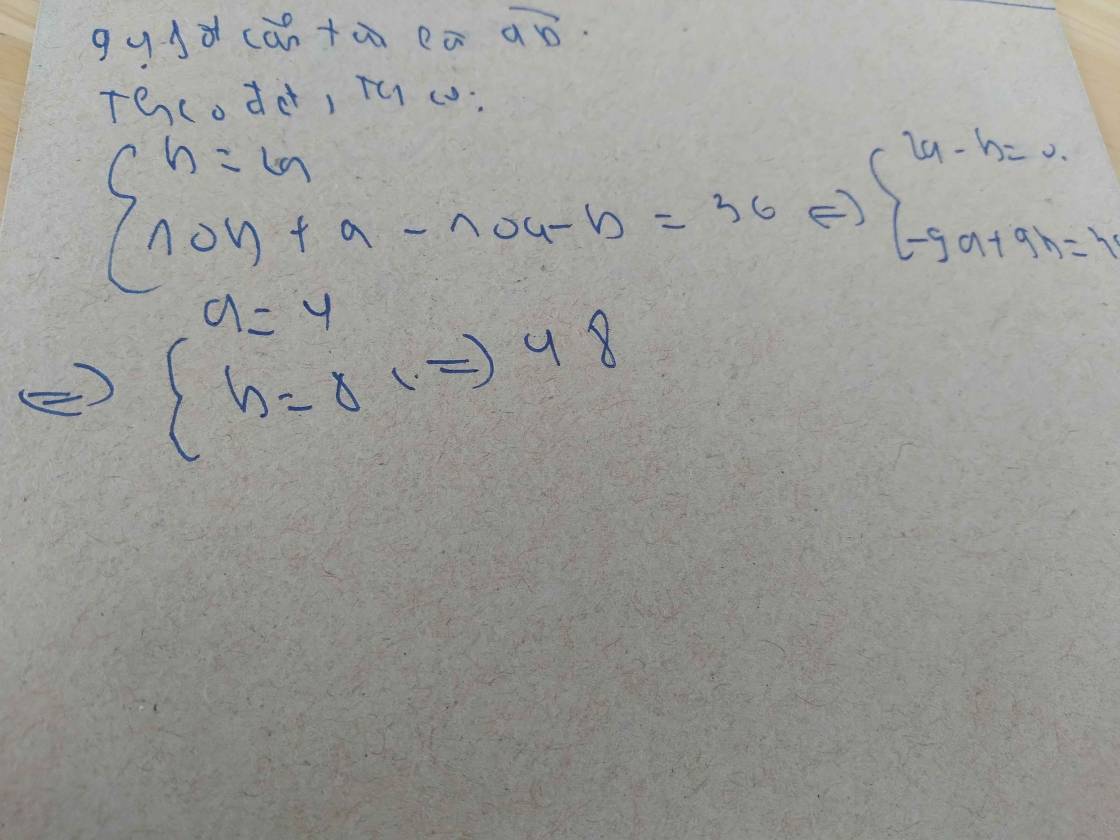
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

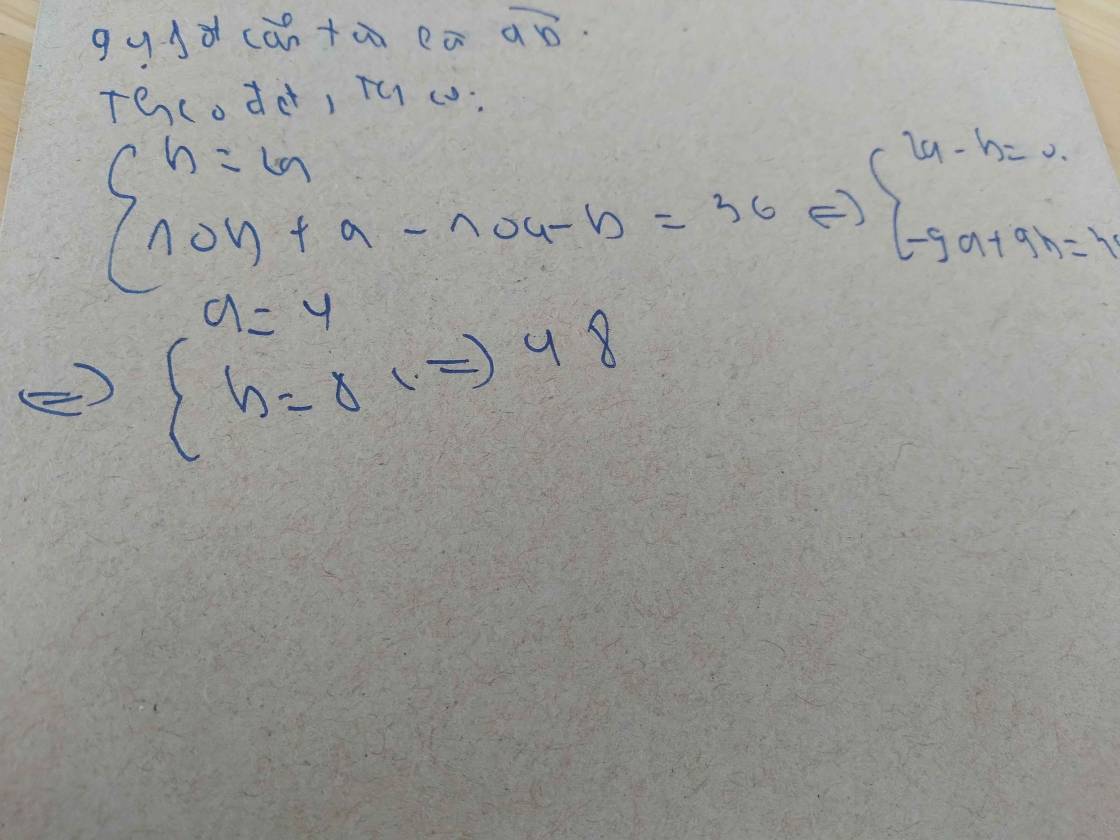

Gọi số cần tìm là 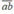 = 10a + b (a, b ∈ N. 0 < a < b < 10)
= 10a + b (a, b ∈ N. 0 < a < b < 10)
Ta có b = 3a
Khi đổi hai chữ số ta được số 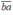 = 10b + a
= 10b + a
Vì số mới lớn hơn số cũ 54 đơn vị nên ta có phương trình: 10b + a – 54 = 10a + b
⇔ 9b – 9a = 54
⇔ 9.3a – 9a = 54
⇔ 18a = 54
⇔ a =3 (tmđk)
Vậy số ban đầu cần tìm là 39.

Gọi \(\overline{ab}\)là số tự nhiên cần tìm (0 < a < 9; 0 < b < 9)
Ta có: \(\overline{a9b}-\overline{ab}=810\)
<=> \(\left(100a+90+b\right)-\left(10a+b\right)=810\)
<=> \(100a+90+b-10a-b=810\)
<=> \(90a+90=810\)
<=> \(90\left(a+1\right)=810\)
<=> \(a+1=9\)
<=> \(a=8\)
và \(a=2b\)
=> \(b=\frac{a}{2}=\frac{8}{2}=4\)
Vậy số ban đầu là số 84.

Gọi số ban đầu là \(\overline{ab}\)
Theo đề, ta có:
a=2b và 10a+b-10b-a=36
=>a-2b=0 và a-b=4
=>a=8 và b=4

Gọi số cần tìm có dạng là \(\overline{ab}\)
Theo đề, ta có hệ: b=2a và 10b+a-10a-b=18
=>2a-b=0 và -9a+9b=18
=>a=2 và b=4

Gọi số cần tìm là \(ab\left(ab\in N.0< a< b< 10\right)\)
Ta có : \(b=3a\)
Khi đổi hai chữ số ta được số \(ba=10b+a\)
Vì số mới lớn hơn số cũ 54 đơn vị nên ta có phương trình:
\(10b+a-54=10a+b\)
\(\Leftrightarrow9b-9a=54\)
\(\Leftrightarrow9.3a-9a=54\)
\(\Leftrightarrow18a=54\)
\(\Leftrightarrow a=3\left(tm\right)\)
Mà \(b=3a\) nên \(b=3\times3=9\left(tm\right)\)
Vậy số cần tìm là \(39\)

* Phân tích:
Với một số có hai chữ số bất kì ta luôn có: 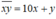
Khi thêm chữ số 1 xen vào giữa ta được số: 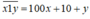
Vì chữ số hàng đơn vị gấp 2 lần chữ số hàng chục nên ta có y = 2x.
Số mới lớn hơn số ban đầu 370 nên ta có phương trình:
100x + 10 + 2x = 10x + 2x + 370.
* Giải:
Gọi chữ số hàng chục của số cần tìm là x (x ∈ N; 0 < x ≤ 9).
⇒ Chữ số hàng đơn vị là 2x
⇒ Số cần tìm bằng 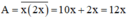
Sau khi viết thêm chữ số 1 vào giữa hai chữ số ta được số mới là:
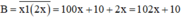
Theo đề bài số mới lớn hơn số ban đầu 370, ta có B = A + 370 nên ta có phương trình
102x + 10 = 12x + 370
⇔ 102x – 12x = 370 – 10
⇔ 90x = 360
⇔ x = 4 (thỏa mãn)
Vậy số cần tìm là 48.
*Lưu ý : Vì chỉ có 4 số có hai chữ số thỏa mãn điều kiện chữ số hàng đơn vị gấp đôi chữ số hàng chục là : 12 ; 24 ; 36 ; 48 nên ta có thể đi thử trực tiếp mà không cần giải bằng cách lập phương trình.