1 . Rút gọn biểu thức M bằng cách hợp lý biết M = (1- 1/4 ) (1- 1/9 ) (1-1/16 )........(1-1/900)
giúp em với mọi người oi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(M=\left(1-\dfrac{1}{4}\right)\left(1-\dfrac{1}{9}\right)\left(1-\dfrac{1}{16}\right)...\left(1-\dfrac{1}{900}\right)\)
\(=\left(1-\dfrac{1}{2^2}\right)\left(1-\dfrac{1}{3^2}\right)\left(1-\dfrac{1}{4^2}\right)...\left(1-\dfrac{1}{30^2}\right)\)
\(=\left(\dfrac{2^2-1}{2^2}\right)\left(\dfrac{3^2-1}{3^2}\right)\left(\dfrac{4^2-1}{4^2}\right)...\left(\dfrac{30^2-1}{30^2}\right)\)
\(=\left(\dfrac{1.3}{2^2}\right)\left(\dfrac{2.4}{3^2}\right)\left(\dfrac{3.5}{4^2}\right)...\left(\dfrac{29.31}{30^2}\right)\)
\(=\left(\dfrac{1.2.3...29}{2.3.4...30}\right).\left(\dfrac{3.4.5...31}{2.3.4...30}\right)=\dfrac{1}{30}.\dfrac{31}{2}=\dfrac{31}{60}\)

Ta có: \(\left(1-\frac{1}{1007}\right)\times\left(1-\frac{1}{1008}\right)\times...\times\left(1-\frac{1}{1011}\right)\times\left(1-\frac{1}{1012}\right)\)
\(=\frac{1006}{1007}\times\frac{1007}{1008}\times...\times\frac{1010}{1011}\times\frac{1011}{1012}\)
\(=\frac{1006}{1012}=\frac{503}{506}\)
\(\left(1-\frac{1}{1007}\right)\cdot\left(1-\frac{1}{1008}\cdot\right)...\cdot\left(1-\frac{1}{1011}\right)\cdot\left(1-\frac{1}{1012}\right)\)
\(=\frac{1006}{1007}\cdot\frac{1007}{1008}\cdot...\cdot\frac{1010}{1011}\cdot\frac{1011}{1012}\)
\(=\frac{1006.1007\cdot..\cdot2010\cdot2011}{1007\cdot1008\cdot....\cdot1011.1012}\)
\(=\frac{1006}{1012}\)
\(=\frac{503}{506}\)

Lời giải:
\(A=\frac{2a^2+4}{(1-a)(1+a)}-\frac{1-\sqrt{a}+1+\sqrt{a}}{(1+\sqrt{a})(1-\sqrt{a})}=\frac{2a^2+4}{(1-a)(1+a)}-\frac{2}{1-a}\)
\(=\frac{2a^2+4}{(1-a)(1+a)}-\frac{2(1+a)}{(1-a)(1+a)}=\frac{2a^2-2a+2}{(1-a)(1+a)}=\frac{2(a^2-a+1)}{1-a^2}\)


\(a,B=4\sqrt{x=1}-3\sqrt{x+1}+2\)\(\sqrt{x+1}+\sqrt{x+1}\)
\(=4\sqrt{x+1}\)
\(b,\)đưa về \(\sqrt{x+1}=4\Rightarrow x=15\)
a, Với \(x\ge-1\)
\(\Rightarrow B=4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}\)
\(=4\sqrt{x+1}\)
b, Ta có B = 16 hay
\(4\sqrt{x+1}=16\Leftrightarrow\sqrt{x+1}=4\)bình phương 2 vế ta được
\(\Leftrightarrow x+1=16\Leftrightarrow x=15\)

Ta có: \(\left(3+1\right)\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\)
\(=\dfrac{\left(3-1\right)\left(3+1\right)\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)}{2}\)
\(=\dfrac{\left(3^2-1\right)\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)}{2}\)
\(=\dfrac{\left(3^4-1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)}{2}\)
\(=\dfrac{\left(3^8-1\right)\left(3^8+1\right)\left(3^{16}+1\right)}{2}\)
\(=\dfrac{\left(3^{16}-1\right)\left(3^{16}+1\right)}{2}\)
\(=\dfrac{3^{32}-1}{2}\)
Rút gọn: (3 + 1)(32 + 1)(34 + 1)(38 + 1)(316 + 1)(332 + 1)
A=(3 + 1)(32 + 1)(34 + 1)(38 + 1)(316 + 1)(332 + 1)
A=(3-1)(3 + 1)(32 + 1)(34 + 1)(38 + 1)(316 + 1)(332 + 1)
A=(32-1)(32 + 1)(34 + 1)(38 + 1)(316 + 1)(332 + 1)
A=(34-1)(34 + 1)(38 + 1)(316 + 1)(332 + 1)
A=(38-1)(38 + 1)(316 + 1)(332 + 1)
A=(316-1)(316 + 1)(332 + 1)
A=(332 - 1)(332 + 1)
A=364-1
=>A=(364-1) /2
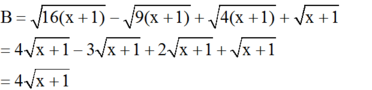
\(1-\dfrac{1}{n^2}=\dfrac{n^2-1}{n^2}=\dfrac{\left(n-1\right)\left(n+1\right)}{n^2}\)
Do đó:
\(M=\left(1-\dfrac{1}{2^2}\right)\left(1-\dfrac{1}{3^2}\right)\left(1-\dfrac{1}{4^2}\right)...\left(1-\dfrac{1}{30^2}\right)\)
\(=\dfrac{\left(2-1\right)\left(2+1\right)}{2^2}.\dfrac{\left(3-1\right)\left(3+1\right)}{3^2}.\dfrac{\left(4-1\right)\left(4+1\right)}{4^2}...\dfrac{\left(30-1\right)\left(30+1\right)}{30^2}\)
\(=\dfrac{1.3}{2^2}.\dfrac{2.4}{3^2}.\dfrac{3.5}{4^2}...\dfrac{29.31}{30^2}=\dfrac{1.2.3...29}{2.3.4...30}.\dfrac{3.4.5...31}{2.3.4...30}\)
\(=\dfrac{1}{30}.\dfrac{31}{2}=\dfrac{31}{60}\)