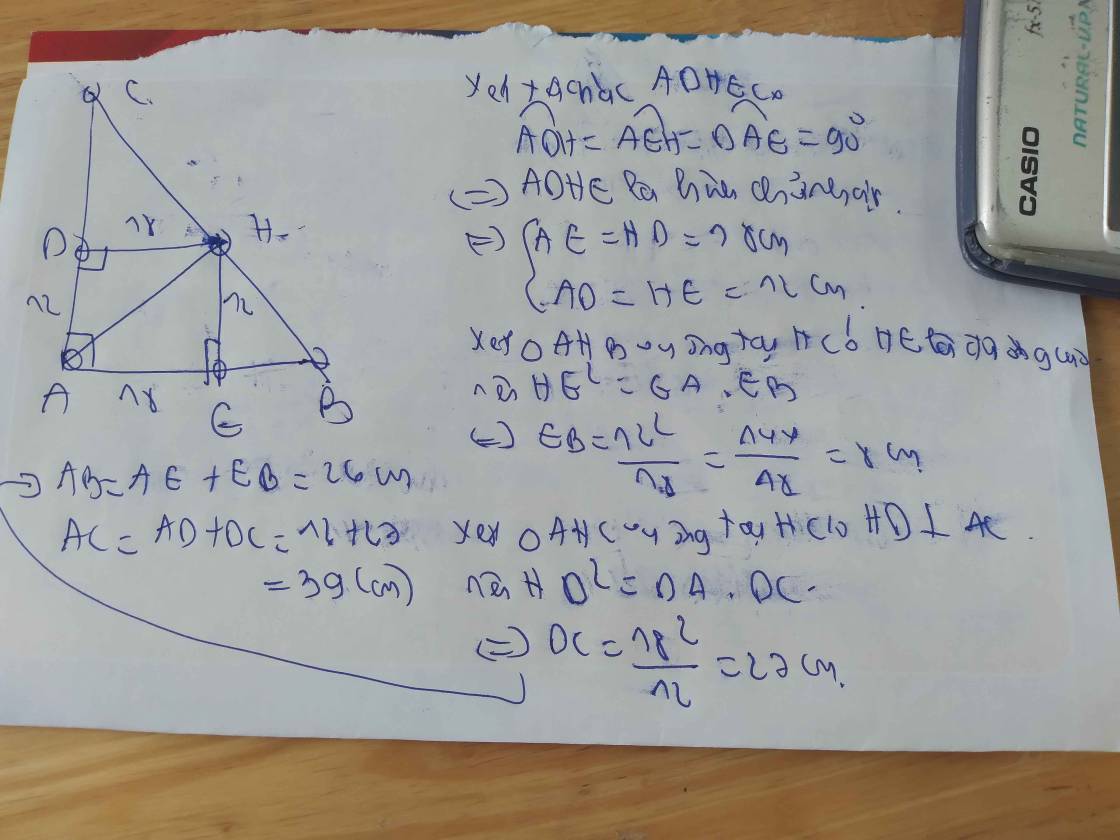
Cho tam giác ABC vuông tại A,đường cao AH.Gọi D là hình chiếu của H trên AC ,gọi E là hình chiếu của H trên AB.Biết HD bằng 18cm,HE bằng 12cm.Tính độ dài các cạnh AB,AC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KT
16 tháng 7 2018
Dễ dàng chứng minh được: \(HEAD\)là hình chữ nhật
\(\Rightarrow\)\(HE=AD=12\)
\(HD=EA=18\)
Áp dụng hệ thức lượng ta có:
\(HD^2=AD.DC\)
\(\Rightarrow\)\(DC=\frac{HD^2}{AD}\)
\(\Rightarrow\)\(DC=\frac{18^2}{12}=27\)
\(\Rightarrow\)\(AC=AD+DC=12+27=39\)
\(HE^2=BE.AE\)
\(\Rightarrow\)\(BE=\frac{HE^2}{AE}\)
\(\Rightarrow\)\(BE=\frac{12^2}{18}=8\)
\(\Rightarrow\)\(AB=BE+EA=8+18=26\)
22 tháng 10 2023
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=9^2+12^2=15^2\)
=>BC=15(cm)
Xét ΔABC vuông tại A có
\(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
=>\(\widehat{C}\simeq37^0\)
=>\(\widehat{B}=90^0-\widehat{C}=53^0\)
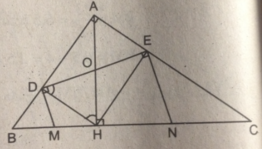
b: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
=>AH=EF
ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
c: ΔABC vuông tại A có AK là đường trung tuyến
nên KA=KB=KC
KA=KC
=>\(\widehat{KAC}=\widehat{KCA}\)
\(\widehat{AFE}+\widehat{KAC}\)
\(=\widehat{AHE}+\widehat{KCA}\)
\(=\widehat{ABC}+\widehat{ACB}=90^0\)
=>AK vuông góc EF
CM
1 tháng 11 2017
Xét hai tam giác vuông ABH và CAH có:
∠ ABH = ∠ CAH (cùng phụ với góc ∠ BAH)
Do đó △ ABH đồng dạng △ CAH (g.g).
Suy ra: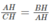 
⇒ A H 2 = BH. CH = 4.9 = 36 ⇒ AH = 6(cm)
Mặt khác, HD ⊥ AB và HE ⊥ AC nên ADHE là hình chữ nhật.
Suy ra: DE = AH = 6 (cm)
26 tháng 8 2022
Câu 1:
a: Xét ΔAHB vuông tạiH có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
b: \(BC=\sqrt{4^2+6^2}=2\sqrt{13}\left(cm\right)\)
\(AH=\dfrac{4\cdot6}{2\sqrt{13}}=\dfrac{12}{\sqrt{13}}\left(cm\right)\)
\(AE=\dfrac{AH^2}{AC}=\dfrac{144}{13}:6=\dfrac{24}{13}\left(cm\right)\)