Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

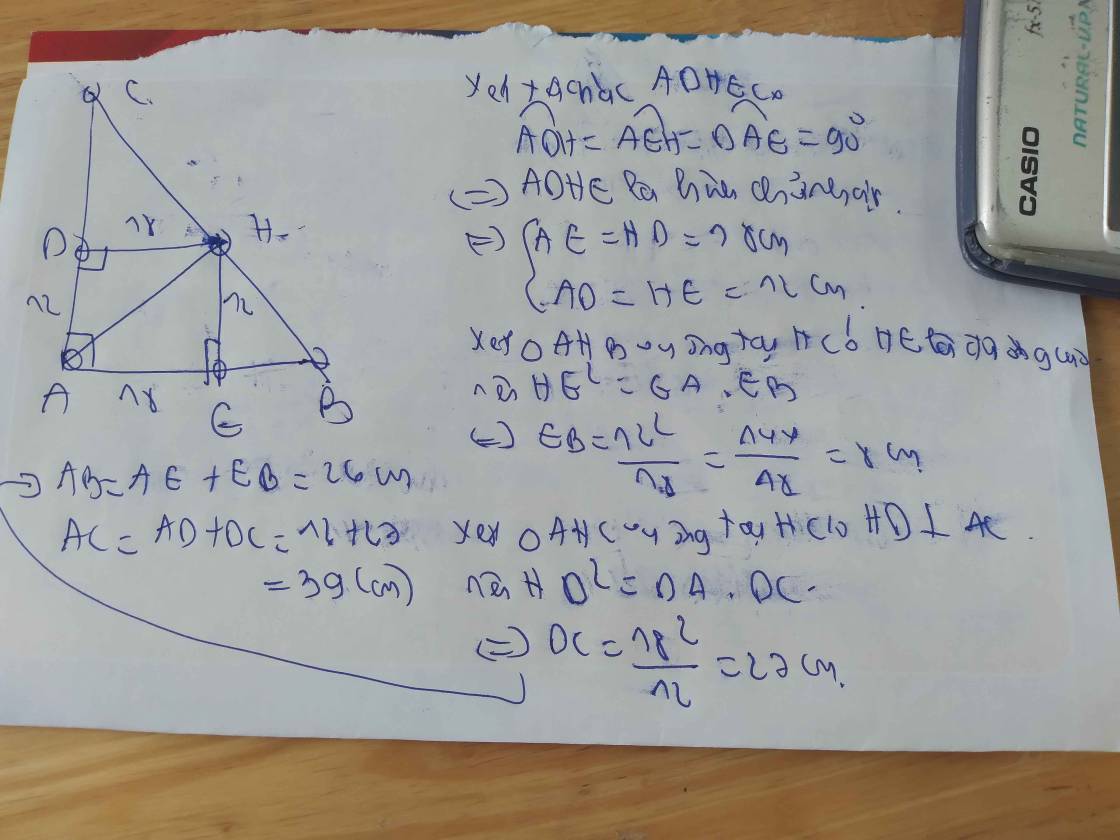
Dễ dàng chứng minh được: \(HEAD\)là hình chữ nhật
\(\Rightarrow\)\(HE=AD=12\)
\(HD=EA=18\)
Áp dụng hệ thức lượng ta có:
\(HD^2=AD.DC\)
\(\Rightarrow\)\(DC=\frac{HD^2}{AD}\)
\(\Rightarrow\)\(DC=\frac{18^2}{12}=27\)
\(\Rightarrow\)\(AC=AD+DC=12+27=39\)
\(HE^2=BE.AE\)
\(\Rightarrow\)\(BE=\frac{HE^2}{AE}\)
\(\Rightarrow\)\(BE=\frac{12^2}{18}=8\)
\(\Rightarrow\)\(AB=BE+EA=8+18=26\)

b: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật
Suy ra: AH=EF(1)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AH^2=BH\cdot CH\left(2\right)\)
Từ (1) và (2) suy ra \(FE^2=BH\cdot CH\)

a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
hay AH=7,2(cm)