tim gia tri nho nhat cua 2x-5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Vì |x-3| luôn lớn bằng 0 với mọi x
=> |x - 3| + (-100) luôn lớn bằng -100 với mọi x
=> A luôn lớn bằng 100
Dấu "=" xảy ra <=> |x-3| = 0
=> x - 3 = 0
=> x = 3
Vậy Min A = -100 <=> x = 3
Ta có |x - 3| > 0
=> |x - 3| + (-100) > - 100
hay A > 100
Vậy GTNN của A là 100 <=> |x - 3| = 0 <=> x - 3 = 0 <=> x = 3

D= 2x2 - 6x
= 2(x2 - 3x +\(\dfrac{9}{4}\)) - \(\dfrac{9}{2}\)
= 2[x2 - 2.x.\(\dfrac{3}{2}\) + (\(\dfrac{3}{2}\))2 ] - \(\dfrac{9}{2}\)
= 2 (x - \(\dfrac{3}{2}\))2 - \(\dfrac{9}{2}\)
Ta có:
2(x - \(\dfrac{3}{2}\))2 ≥ 0 ⇒ 2 (x - \(\dfrac{3}{2}\))2 - \(\dfrac{9}{2}\) ≥ -\(\dfrac{9}{2}\)
Hay D≥ -\(\dfrac{9}{2}\)
Dấu = xảy ra ⇔ (x - \(\dfrac{3}{2}\)) = 0 ⇔ x = \(^{\dfrac{3}{2}}\)
Vậy MinD = - \(\dfrac{9}{2}\) ⇔ x = \(\dfrac{3}{2}\)

\(P=\frac{x^2-2x+1989}{x^2}\)
\(\Leftrightarrow Px^2=x^2-2x+1989\)
\(\Leftrightarrow x^2\left(1-P\right)-2x+1989=0\)
\(\Delta=4-4\left(1-P\right)1989\ge0\)
\(\Leftrightarrow P\ge\frac{1988}{1989}\)có GTNN là \(\frac{1988}{1989}\)
Dấu "=" xảy ra \(\Leftrightarrow x=1989\)
Vậy \(P_{min}=\frac{1988}{1989}\) tại x = 1989

Vì |y + 3| luôn lớn bằng 0 với mọi y
=> 100 - |y + 3| luôn bé bằng 0
=> B luôn bé bằng 0
Dấu "=" xảy ra <=> |y + 3| = 0
=> y + 3 = 0
=> y = -3
Vậy Max B = 100 tại y = -3
Ta có - |y - 3| < 0
=> B = 100 - |y - 3| < 100
GTLN của B là 100 <=> |y - 3| = 0 <=> y = 3

2.E = 4x^2 - 12x
= ( 4x^2 - 12x + 9 ) -9
=(2x-3)^2 - 9 >= -9
<=> E >= -18
Dấu "=" xảy ra <=> 2x-3 = 0 <=> x=3/2
Vậy GTNN của E là E = -18 <=> x =3/2
Ta có : E = 2x2 - 6x
=> E = 2(x2 - 6x + 9 - 9)
=> E = 2(x2 - 6x + 9) - 18
=> E = 2(x - 3)2 - 18
Mà ; 2(x - 3)2 \(\ge0\forall x\)
Nên: E = 2(x - 3)2 - 18 \(\ge-18\forall x\)
Vậy Emin = -18 khi x = 3
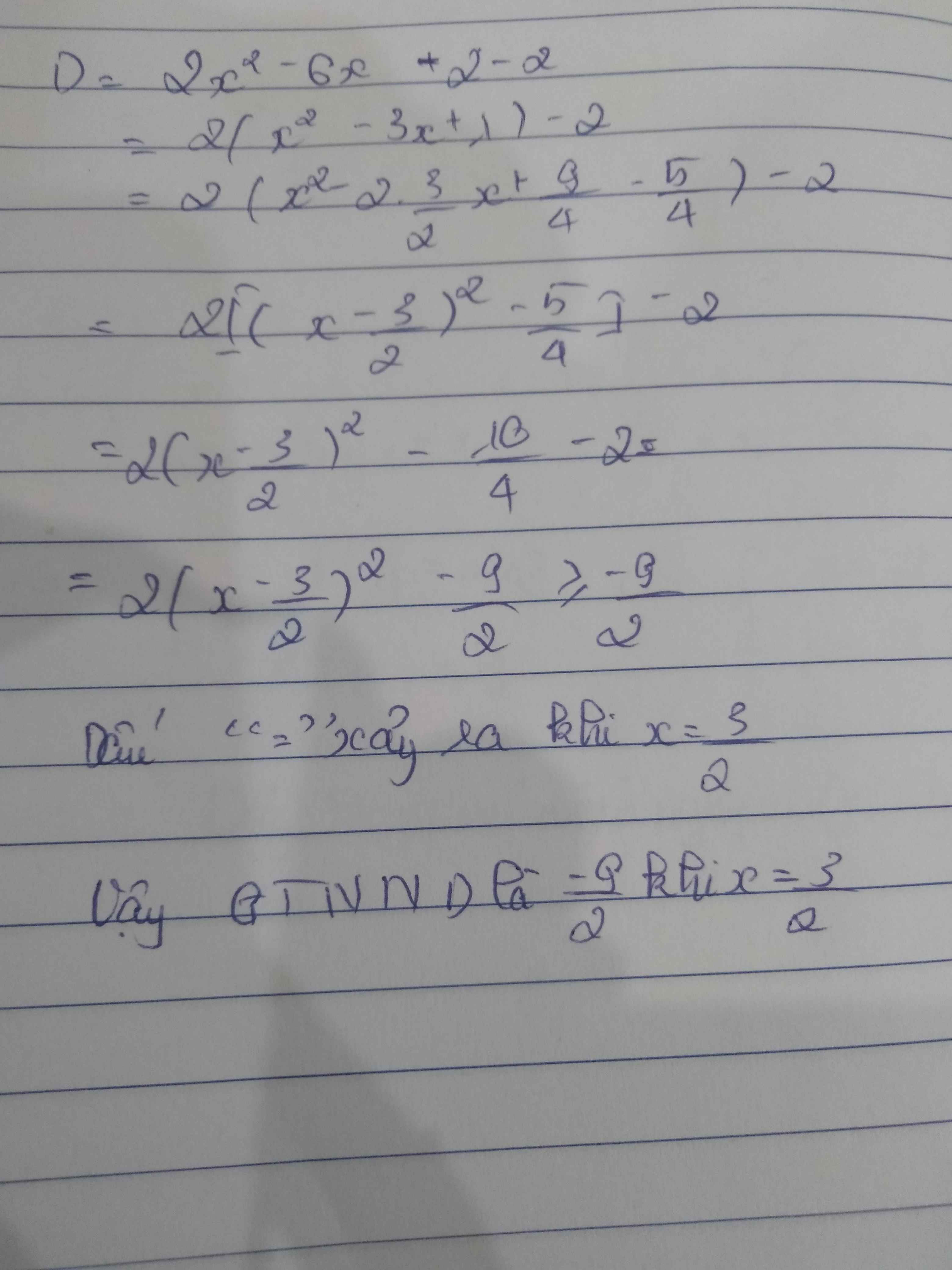
fgfgfgf
2x-5
=>x=3