Cho tam giác $ABC$ vuông ở $A$ có $AB = 8$, $AC = 15$. Vẽ đường cao $AH$. Gọi $D$ là điểm đối xứng với $B$ qua $H$. Vẽ đường tròn đường kính $CD$, cắt $AC$ ở $E$.
a) Chứng minh rằng $HE$ là tiếp tuyến của đường tròn.
b) Tính độ dài $HE$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Gọi M là trung điểm của CD
=>ΔCED nội tiếp đường tròn đường kính CD có M là tâm
=>MD=ME
=>ΔMDE cân tại M
=>góc MED=góc MDE
Xét ΔABD có
AH vừa là đường cao, vừa là đường trung tuyến
nên ΔABD cân tại A
=>AH là phân giác của góc BAD
=>góc BAH=góc DAH
Xét tứ giác AHDE có
góc AHD+góc AED=180 độ
nên AHDE là tứ giác nội tiếp
=>góc DAH=góc DEH
=>góc DEH=góc BAH=góc C
=>góc MEH=góc C+góc CDE=90 độ
=>HE là tiếp tuyến của (M)
b: \(HB=DH=\dfrac{AB^2}{BC}=\dfrac{64}{17}\left(cm\right)\)
CD=BC-2x64/17=161/17(cm)
EM=161/17:2=161/34(cm)
MH=MD+DH=BC/2=8,5cm
=>\(HE=\sqrt{MH^2-EM^2}=\dfrac{120}{17}\left(cm\right)\)

a: Gọi M là trung điểm của CD
=>ΔCED nội tiếp đường tròn đường kính CD có M là tâm
=>MD=ME
=>ΔMDE cân tại M
=>góc MED=góc MDE
Xét ΔABD có
AH vừa là đường cao, vừa là đường trung tuyến
nên ΔABD cân tại A
=>AH là phân giác của góc BAD
=>góc BAH=góc DAH
Xét tứ giác AHDE có
góc AHD+góc AED=180 độ
nên AHDE là tứ giác nội tiếp
=>góc DAH=góc DEH
=>góc DEH=góc BAH=góc C
=>góc MEH=góc C+góc CDE=90 độ
=>HE là tiếp tuyến của (M)
b: \(HB=DH=\dfrac{AB^2}{BC}=\dfrac{64}{17}\left(cm\right)\)
CD=BC-2x64/17=161/17(cm)
EM=161/17:2=161/34(cm)
MH=MD+DH=BC/2=8,5cm
=>\(HE=\sqrt{MH^2-EM^2}=\dfrac{120}{17}\left(cm\right)\)

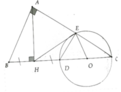
a, Gọi O là trung điểm CD
Từ giả thiết suy ra tam giác ABD và tam giác ODE đều
=> DE = DH = DO = 1 4 BC
=> H E O ^ = 90 0
=> HE là tiếp tuyến của đường tròn đường kính CD
b, HE = 4 3
a: Gọi M là trung điểm của CD
=>ΔCED nội tiếp đường tròn đường kính CD có M là tâm
=>MD=ME
=>ΔMDE cân tại M
=>góc MED=góc MDE
Xét ΔABD có
AH vừa là đường cao, vừa là đường trung tuyến
nên ΔABD cân tại A
=>AH là phân giác của góc BAD
=>góc BAH=góc DAH
Xét tứ giác AHDE có
góc AHD+góc AED=180 độ
nên AHDE là tứ giác nội tiếp
=>góc DAH=góc DEH
=>góc DEH=góc BAH=góc C
=>góc MEH=góc C+góc CDE=90 độ
=>HE là tiếp tuyến của (M)
b: \(HB=DH=\dfrac{AB^2}{BC}=\dfrac{64}{17}\left(cm\right)\)
CD=BC-2x64/17=161/17(cm)
EM=161/17:2=161/34(cm)
MH=MD+DH=BC/2=8,5cm
=>\(HE=\sqrt{MH^2-EM^2}=\dfrac{120}{17}\left(cm\right)\)

a: Gọi M là trung điểm của CD
=>ΔCED nội tiếp đường tròn đường kính CD có M là tâm
=>MD=ME
=>ΔMDE cân tại M
=>góc MED=góc MDE
Xét ΔABD có
AH vừa là đường cao, vừa là đường trung tuyến
nên ΔABD cân tại A
=>AH là phân giác của góc BAD
=>góc BAH=góc DAH
Xét tứ giác AHDE có
góc AHD+góc AED=180 độ
nên AHDE là tứ giác nội tiếp
=>góc DAH=góc DEH
=>góc DEH=góc BAH=góc C
=>góc MEH=góc C+góc CDE=90 độ
=>HE là tiếp tuyến của (M)
b: \(HB=DH=\dfrac{AB^2}{BC}=\dfrac{64}{17}\left(cm\right)\)
CD=BC-2x64/17=161/17(cm)
EM=161/17:2=161/34(cm)
MH=MD+DH=BC/2=8,5cm
=>\(HE=\sqrt{MH^2-EM^2}=\dfrac{120}{17}\left(cm\right)\)

a: Gọi M là trung điểm của CD
=>ΔCED nội tiếp đường tròn đường kính CD có M là tâm
=>MD=ME
=>ΔMDE cân tại M
=>góc MED=góc MDE
Xét ΔABD có
AH vừa là đường cao, vừa là đường trung tuyến
nên ΔABD cân tại A
=>AH là phân giác của góc BAD
=>góc BAH=góc DAH
Xét tứ giác AHDE có
góc AHD+góc AED=180 độ
nên AHDE là tứ giác nội tiếp
=>góc DAH=góc DEH
=>góc DEH=góc BAH=góc C
=>góc MEH=góc C+góc CDE=90 độ
=>HE là tiếp tuyến của (M)
b: \(HB=DH=\dfrac{AB^2}{BC}=\dfrac{64}{17}\left(cm\right)\)
CD=BC-2x64/17=161/17(cm)
EM=161/17:2=161/34(cm)
MH=MD+DH=BC/2=8,5cm
=>\(HE=\sqrt{MH^2-EM^2}=\dfrac{120}{17}\left(cm\right)\)

Gọi M là trung điểm của CD
=>M là tâm của đường tròn đường kính CD
=>E thuộc (M)
Xét (M) có
ΔCED nội tiếp
CD là đường kính
Do đó: ΔCED vuông tại E
=>DE\(\perp\)EC tại E
=>DE\(\perp\)AC tại E
Xét ΔABD có
AH là đường cao
AH là đường trung tuyến
Do đó: ΔABD cân tại A
TA có: ΔABD cân tại A
mà AH là đường cao
nên AH là phân giác của góc BAD
=>\(\widehat{BAH}=\widehat{DAH}\)
Xét tứ giác AHDE có
\(\widehat{AHD}+\widehat{AED}=90^0+90^0=180^0\)
=>AHDE là tứ giác nội tiếp
=>\(\widehat{DEH}=\widehat{DAH}\)
mà \(\widehat{DAH}=\widehat{BAH}\)
nên \(\widehat{DEH}=\widehat{BAH}\)
mà \(\widehat{BAH}=\widehat{C}\left(=90^0-\widehat{ABC}\right)\)
nên \(\widehat{DEH}=\widehat{C}\)
Ta có: ME=MD
=>ΔMED cân tại M
=>\(\widehat{MED}=\widehat{MDE}\)
=>\(\widehat{MED}=\widehat{CDE}\)
\(\widehat{HEM}=\widehat{HED}+\widehat{MED}\)
\(=\widehat{CDE}+\widehat{C}\)
\(=90^0\)
=>HE\(\perp\)EM tại E
Xét (M) có
ME là bán kính
HE\(\perp\)ME tại E
Do đó: HE là tiếp tuyến của (M)

a) E nằm trên đường tròn đường kính CD
=> Tam giác CDE vuông tại E
=> DE // AB
Gọi M là trung điểm của AE
HM là đường trung bình của hình thang ABDE
=> HM // AB => \(HM\perp AB\)
=> Tam giác AHE cân tại H => \(\widehat{AEH}=\widehat{EAH}\)
Tam giác COE cân tại O => \(\widehat{OEC}=\widehat{OCE}\)
=> \(\widehat{OEC}+\widehat{AEH}=\widehat{OCE}+\widehat{EAH}=90^o\)
=> \(HE\perp OE\)=> Đpcm
b) Tam giác ABC vuông tại A
=> \(BC^2=AB^2+AC^2=289\)
=> BC = 17
Tam giác ABC vuông tại A, đường cao AH
=> AB . AC = AH . BC
=> \(HE=AH=\frac{120}{17}\)
a) Gọi O là trung điểm của CD.
Do E nằm trên đường tròn (O) nên ^DEC=90o hay DE⊥AC.
Thế thì DE//AB.
Gọi M là trung điểm AE, xét hình thang ABDE có: H là trung điểm BD và M là trung điểm AE nên HM là đường trung bình của hình thang.
Vậy nên HM//AB//DE hay HM⊥AE.
Suy ra tam giác HAE cân tại H hay ^HEA=^HAE.
Tam giác OEC cân tại O nên ^OEC=^OCE.
Từ đó ta có: ^HEA+^OEC=^HAE+^OCE=90o.
Suy ra ^OEH=180o−90o=90o.
Vậy nên HEHE là tiếp tuyến của đường tròn (O).
b) Xét tam giác ABC vuông tại A, áp dụng định lý Pi-ta-go, ta có:
BC=√AB2+AC2=17(cm)
Do tam giác HAE cân tại H nên:
HE = AH = (AB*AC)/BC=120/17
a) Gọi O là trung điểm của CD.
Do E nằm trên đường tròn (O) nên \widehat{DEC}=90^oDEC=90o hay DE\perp ACDE⊥AC.
Thế thì DE//AB.
Gọi M là trung điểm AE, xét hình thang ABDE có: H là trung điểm BD và M là trung điểm AE nên HM là đường trung bình của hình thang.
Vậy nên HM//AB//DE hay HM\perp AE.HM⊥AE.
Suy ra tam giác HAE cân tại H hay \widehat{HEA}=\widehat{HAE}HEA=HAE.
Tam giác OEC cân tại O nên \widehat{OEC}=\widehat{OCE}OEC=OCE.
Từ đó ta có: \widehat{HEA}+\widehat{OEC}=\widehat{HAE}+\widehat{OCE}=90^o.HEA+OEC=HAE+OCE=90o.
Suy ra \widehat{OEH}=180^o-90^o=90^o.OEH=180o−90o=90o.
Vậy nên HEHE là tiếp tuyến của đường tròn (O).
b) Xét tam giác ABC vuông tại A, áp dụng định lý Pi-ta-go, ta có:
BC=\sqrt{AB^2+AC^2}=17\left(cm\right)BC=AB2+AC2=17(cm)
Do tam giác HAE cân tại H nên:
HE = AH = \dfrac{AB.AC}{BC}=\dfrac{120}{17}.BCAB.AC=17120.