Tìm tất cả các nghiệm nguyên của phương trình \(10x+13y=16\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giả sử x;y là các số nguyên thỏa mãn phương trình 2x + 13y = 156
2x + 13y = 156 ⇒ 2x = 156 - 13y
Ta nhận thấy 13y và 156 đều chia hết cho 13.
Do đó 2x ⋮ 13
Đặt x = 13t (t ∈ Z) thay vào phương trình ta được:
2.13t + 13y = 156 ⇔ 26t + 13y = 156 ⇔ 2t + y = 12 ⇔ y = - 2t + 12
Vậy nghiệm nguyên của phương trình là (x = 13t; y = - 2t + 12) (với t ∈ Z)
Đáp án D
Phương trình tương đương với 4 4 x + 1 4 x = 4 ( m + 1 ) 2 x - 1 2 x + 16 - 8 m
⇔ 4 x + 1 4 x = ( m + 1 ) 2 x - 1 2 x + 4 - 2 m (1)
Đặt 2 x - 1 2 x = t → 4 x + 1 4 x = t 2 + 2 . Xét hàm số t ( x ) = 2 x - 1 2 x trên 0 ; 1 .
Đạo hàm t ' ( x ) = 2 x . ln 2 + ln 2 2 x > 0 , ∀ x ∈ 0 ; 1 ⇒ Hàm số t (x) luôn đồng biến trên [0;1]. Suy ra m i n x ∈ [ 0 ; 1 ] t ( x ) = t ( 0 ) = 0 và m a x x ∈ [ 0 ; 1 ] t ( x ) = t ( 1 ) = 3 2 . Như vậy t ∈ 0 ; 3 2 .
Phương trình (1) có dạng: t 2 + 2 = ( m + 1 ) t + 4 - 2 m ⇔ t 2 - ( m + 1 ) t + 2 m = 0
⇔ ( t - 2 ) t + 1 - m = 0 ⇔ t = 2 ∉ 0 ; 3 2 t = m - 1
Phương trình (1) có nghiệm x ∈ 0 ; 1 ⇔ phương trình ẩn t có nghiệm
t ∈ 0 ; 3 2 ⇔ 0 ≤ m - 1 ≤ 3 2 ⇔ 1 ≤ m ≤ 5 2 . Mà m ∈ ℤ nên m ∈ 1 ; 2 . Tổng tất cả các giá trị nguyên của m bằng 3.

Đáp án D.
Phương trình tương đương với

Đặt 2 x - 1 2 x = t → 4 x + 1 4 x = t 2 + 2 . Xét hàm số t ( x ) = 2 x - 1 2 x trên 0 ; 1 .
Đạo hàm t ' ( x ) = 2 x . ln 2 + ln 2 2 x > 0 , ∀ x ∈ 0 ; 1 ⇒ Hàm số t ( x ) luôn đồng biến trên 0 ; 1 . Suy ra min x ∈ 0 ; 1 t ( x ) = t ( 0 ) = 0 và max x ∈ 0 ; 1 t ( x ) = t ( 1 ) = 3 2 . Như vậy t ∈ 0 ; 3 2 .
Phương trình (1) có dạng:
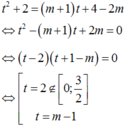
Phương trình (1) có nghiệm t ∈ 0 ; 1 ⇔ phương trình ẩn t có nghiệm t ∈ 0 ; 3 2 ⇔ 0 ≤ m - 1 ≤ 3 2 ⇔ 1 ≤ m ≤ 5 2 . Mà m ∈ ℤ nên m ∈ 1 ; 2 . Tổng tất cả các giá trị nguyên của m bằng 3.

a) 5x−13y=7⇔y=5x−713=5x+5−13135x−13y=7⇔y=5x−713=5x+5−1313
=5(x+1)13−1=5(x+1)13−1(1)
đật x+1=13t⇔x=13t−1(t−thuoc−Z)x+1=13t⇔x=13t−1(t−thuoc−Z)
thay vào (1) ta có y=5t−1(t−thuoc−Z)y=5t−1(t−thuoc−Z)
b) 6x−5y=−38⇔x=5y−386=5y+10−4866x−5y=−38⇔x=5y−386=5y+10−486
=5(y+2)6−8=5(y+2)6−8(1)
đặt y+2=6t⇔y=6t−2(t−thuoc−Zy+2=6t⇔y=6t−2(t−thuoc−Z(2)
vì y>0⇒t>13y>0⇒t>13(3)
thay (2) vào (1) ta có;
x=5t−8x=5t−8vì x<0⇒t<85(t−thuoc−Z)x<0⇒t<85(t−thuoc−Z)(4)
từ (3),(4) 13<t<8513<t<85
mà t thuôc Z nên t=1
với t= 1 thì x=-3,y=4



\(pt:x^2-2mx+m-4=0\left(1\right)\)
\(\Delta'=\left(-m\right)^2-\left(m-4\right)=m^2-m+4=m^2-2.\dfrac{1}{2}m+\dfrac{1}{4}-\dfrac{1}{4}+4\)
\(=\left(m-\dfrac{1}{2}\right)^2+\dfrac{15}{6}>0\left(\forall m\right)\)
=> \(pt\left(1\right)\) luôn có 2 nghiệm phân biệt x1,x2 \(\forall m\)
\(Theo\) \(\)Vi ét\(=>\left\{{}\begin{matrix}x1+x2=2m\left(1\right)\\x1x2=m-4\left(2\right)\end{matrix}\right.\)
từ(1)
với \(x1x2=m-4=>m=x1x2+4\)
thay \(m=x1x2+4\) vào (1)\(\)\(=>x1+x2=2\left(x1x2+4\right)\)
\(< =>x1+x2=2x1x2+8\)
\(< =>x1+x2-2x1x2=8\)
\(< =>2x1+2x2-4x1x2=16\)
\(=>2x1\left(1-2x2\right)-\left(1-2x2\right)=15\)
\(< =>\left(2x1-1\right)\left(1-2x2\right)=16\)(3)
để (3) nguyên \(< =>\left(2x1-1\right)\left(1-2x2\right)\inƯ\left(16\right)=\left\{\pm1;\pm2;\pm4;\pm8;\pm16\right\}\)
đến đây bạn tự lập bảng giá trị để tìm x1,x2 rồi từ đó thay thế x1,x2 vào(2) để tìm m nhé (mik ko làm nữa dài lắm)