Cho phương trình ẩn x: x2 – 2mx + 4 = 0 (1)
a) Giải phương trình đã cho khi m = 3.
b) Tìm giá trị của m để phương trình (1) có hai nghiệm x1, x2 thỏa mãn: ( x1 + 1 )2 + ( x2 + 1 )2 = 2.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 2 2022
a, Thay m=0 vào pt ta có:
\(x^2-x+1=0\)
\(\Rightarrow\) pt vô nghiệm
b, Để pt có 2 nghiệm thì \(\Delta\ge0\)
\(\Leftrightarrow\left(-1\right)^2-4.1\left(m+1\right)\ge0\\ \Leftrightarrow1-4m-4\ge0\\ \Leftrightarrow-3-4m\ge0\\ \Leftrightarrow4m+3\le0\\ \Leftrightarrow m\le-\dfrac{3}{4}\)
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=m+1\end{matrix}\right.\)
\(x_1x_2\left(x_1x_2-2\right)=3\left(x_1+x_2\right)\\ \Leftrightarrow\left(x_1x_2\right)^2-2x_1x_2=3.1\\ \Leftrightarrow\left(m+1\right)^2-2\left(m+1\right)-3=0\\ \Leftrightarrow\left[{}\begin{matrix}m+1=3\\m+1=-1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}m=2\left(ktm\right)\\m=-2\left(tm\right)\end{matrix}\right.\)
2 tháng 5 2022
a) Khi \(m=1\) thì pt đã cho trở thành \(x^2-2x-10=0\) (*)
pt (*) có \(\Delta'=\left(-1\right)^2-\left(-10\right)=11>0\)
Do đó (*) có 2 nghiệm phân biệt \(\left[{}\begin{matrix}x_1=\dfrac{-\left(-1\right)+\sqrt{11}}{1}=1+\sqrt{11}\\x_2=\dfrac{-\left(-1\right)-\sqrt{11}}{1}=1-\sqrt{11}\end{matrix}\right.\)
b) Xét pt đã cho \(x^2-mx-10=0\) \(\left(a=1;b=-m;c=-10\right)\)
Nhận thấy \(ac=1\left(-10\right)=-10< 0\) nên pt đã cho luôn có 2 nghiệm phân biệt \(x_1,x_2\).
Áp dụng hệ thức Vi-ét, ta có \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{-m}{1}=m\\x_1x_2=\dfrac{-10}{1}=-10\end{matrix}\right.\)
Ta có \(x_1^2+x_2^2=29\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=29\Leftrightarrow m^2-2\left(-10\right)=29\)\(\Leftrightarrow m^2+20=29\Leftrightarrow m^2=9\Leftrightarrow m=\pm3\)
Vậy để pt đã cho có 2 nghiệm phân biệt thỏa mãn đề bài thì \(m=\pm3\)
9 tháng 3 2018
a, Khi m = 2
pt trở thành : x^2 - 6x + 4 = 0
<=> (x^2-6x+9) - 5 = 0
<=> (x-3)^2 = 5
<=> x=3+-\(\sqrt{5}\)
Tk mk nha
27 tháng 3 2020
b) Câu hỏi của Mavis Dracula - Toán lớp 9 - Học toán với OnlineMath
AH
Akai Haruma
Giáo viên
1 tháng 4 2021
PT $(*)$ là PT bậc nhất ẩn $x$ thì làm sao mà có $x_1,x_2$ được hả bạn?
PT cuối cũng bị lỗi.
Bạn xem lại đề!
CM
10 tháng 8 2018
a) Với m = 1 phương trình trở thành:
x 2 + 4x + 4 = 0 ⇔ (x + 2 ) 2 = 0 ⇔ x = -2
Vậy x = -2
b) Ta có: Δ' = m 2 - 5m + 4
Phương trình có hai nghiệm phân biệt
⇔ Δ' > 0 ⇔
m
2
- 5m + 4 > 0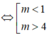 
Do x1 < x2 < 1
27 tháng 4 2019
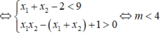
Làm câu b)
Để phương trình có hai nghiệm phân biệt:
\(\Delta'\ge0\Leftrightarrow3^2-\left(m+1\right)\ge0\Leftrightarrow m\le8\)
Áp dụng định lí Vi-ét ta có:
\(\hept{\begin{cases}x_1+x_2=6\\x_1.x_2=m+1\end{cases}}\)(1)
Xét: \(x^2_1+x^2_2=3\left(x_1+x_2\right)\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=3\left(x_1+x_2\right)\)(2)
Từ 1, 2 ta có:
\(6^2-2\left(m+1\right)=3.6\Leftrightarrow m=8\)(tm)
Vậy ...
5 tháng 5 2021
a) Thay m=0 vào phương trình (1), ta được:
\(x^2-2\cdot\left(0-1\right)x+0^2-3m=0\)
\(\Leftrightarrow x^2+2x=0\)
\(\Leftrightarrow x\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
Vậy: Khi m=0 thì S={0;-2}
a, Thay m=3 vào pt ta có:
\(\left(1\right)\Leftrightarrow x^2-6x+4=0\\ \Leftrightarrow x=3\pm\sqrt{5}\)
b, Để pt có 2 nghiệm thì \(\Delta'\ge0\)
\(\Leftrightarrow\left(-m\right)^2-1.4\ge0\\ \Leftrightarrow m^2-4\ge0\\ \Leftrightarrow\left[{}\begin{matrix}m\ge2\\m\le-2\end{matrix}\right.\)
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=4\end{matrix}\right.\)
\(\left(x_1+1\right)^2+\left(x_2+1\right)^2=2\\ \Leftrightarrow x^2_1+2x_1+1+x^2_2+2x_2+1=2\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+2\left(x_1+x_2\right)=0\\ \Leftrightarrow\left(2m\right)^2-2.4+2.2m=0\\ \Leftrightarrow4m^2+4m-8=0\\ \Leftrightarrow\left[{}\begin{matrix}m=1\left(ktm\right)\\m=-2\left(tm\right)\end{matrix}\right.\)