Cho \(\Delta ABC\) và 9 điểm nằm trong tam giác đó. Biết trong 9 điểm đã cho không có 3 điểm nào thẳng hàng. Chứng minh rằng tồn tại ít nhất 3 điểm trong 9 điểm đã cho tạo thành 1 tam giác có diện tích nhỏ hơn 1/4 diện tích tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PN
17 tháng 5 2016
Gọi M ,N ,P lần lượt là trung điểm các cạnh AB ,AC , BC . Do đó \(S_{AMN}=S_{BMP}=S_{ANP}=\frac{1}{4}S_{ABC}\)
Theo nguyên lí di-rich-le thì trong chín điểm đề bài cho, có ít nhất ba điểm nằm trong tam giác AMN,BMP,ANP gọi 3 điểm đó là H , I , K
chẳng hạn 3 điểm H,I,K nằm trong ANP
\(\Rightarrow S_{HIK}< S_{ANP}=\frac{1}{4}S_{ABC}\)
Vậy sẽ có một tâm giác nhỏ hơn 1/4 diện tích tam giác ABC
11 tháng 5 2015
gọi M,N,P lần lượt là trung điểm các cạnh AB,AC,BC
do đó SAMN=SBMP=SANP=1/4 SABC
theo nguyên lý di-rich-le thì trong chín điểm đề bài cho, có ít nhất 3 điểm nằm trong tam giác AMN,BMP hoặc tam giác ANP
gọi 3 điểm đó là H,I,K
chẳng hạn 3 điểm H,I,K nằm trong tam giác ANP
=> SHIK<SANP=1/4 SABC
vậy sẽ có một tam giác nhỏ hơn 1/4 diện tích tam giác ABC
đúng cho mình cái nha!!!
NM
Nguyễn Minh Quang
Giáo viên
9 tháng 8 2021
chia hình vuông thành 25 hình vuông nhỏ có cạnh bằng 1cm ( nghĩa là diện tích bằng 1cm^2)
Theo nguyên lí dirichlet do có 51 điểm và 25 hình vuông
nên tồn tại một hình vuông con chứa ít nhất 3 điểm
Nên 3 điểm đỏ taoh thành 1 tma giác có diện tích nhỏ hơn 1/2 diện tích hình vuông nhỏ là 0,5 cm^2
Vậy ta có điều phải chứng minh
7 tháng 3 2020
làm sao cho chữ màu cam cam zậy bạn???
26 tháng 3 2018
Gọi d là khoảng cách Ai AJ là 2 điểm xa nhau nhất trong các điểm thuộc tập S
Giả sử Ak là điểm xa đường Ai AJ nhất. Ta có tam giác Ai AJAk có diện tích không lớn hơn 1(theo giả thiết). và là tam giác có Smax
Từ các đỉnh Ai, AJ,Ak ta kẻ các đường thẳng song song với các cạnh của tam giác.
Ta sẽ thu được 4 tam giác con bằng nhau và tam giac lớn nhất
Diện tích tam giác lớn nhất này không quá 4 đơn vị
Tam giác lớn nhất này chứa cả 8065 điểm đã cho
(dễ chứng minh bằng phản chứng vì S của tam giác Ai AJAmax)
Vì
8065:4=2016 dư 1
Suy ra tồn tại 1 trong 4 tam giác con chứa không dưới 2017 điểm thuộc tập S thỏa mãn đề bài.
22 tháng 5 2023
Do số tam giác được lập từ n điểm đã cho là hữu hạn nên tồn tại 1 tam giác ABC có diện tích lớn nhất.
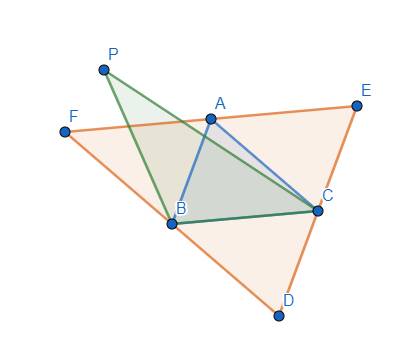
Dựng tam giác DEF sao cho A, B, C lần lượt là trung điểm của EF, DF, DE. Khi đó vì \(S_{ABC}\le1\) nên \(S_{DEF}\le4\). Ta sẽ chứng minh tam giác DEF chính là tam giác cần tìm.
Thật vậy, giả sử tồn tại điểm P trong số n điểm đã cho nằm ngoài tam giác DEF. Không mất tính tổng quát, giả sử P nằm khác phía BC đối với EF. Khi đó khoảng cách từ P đến BC sẽ lớn hơn khoảng cách từ A đến BC, dẫn đến \(S_{PBC}>S_{ABC}\), điều này là vô lí vì ta đã giả sử tam giác ABC là tam giác có diện tích lớn nhất trong số các tam giác tạo thành từ n điểm đã cho \(\Rightarrow\) tam giác DEF thỏa ycbt
Vậy ta có đpcm.
,
21 tháng 5 2023
Nếu bạn không xem được phần trả lời của mình thì vào trang cá nhân của mình xem nhé, tại câu trả lời của mình có vẽ hình nên nó không đăng lên được ngay.
Gọi M,N,P lần lượt là trung điểm các cạnh AB,AC,BC
Do đó diện tích AMN = diện tích BMP = diện tích ANP = \(\frac{1}{4}\) diện tích ABC
Theo nguyên lý di - rich - le thì trong 9 điểm đề bài cho,ít nhất có 3 điểm nằm trong tam giác AMN,BMP hoặc tam giác ANP
Gọi 3 điểm đó là H,I,K
Chẳng hạn 3 điểm H,I,K nằm trong tam giác ANP
= > diện tích HIK < diện tích ANP = \(\frac{1}{4}\) diện tích tam giác ABC
Vậy sẽ có một tam giác nhỏ hơn \(\frac{1}{4}\) diện tích tam giác ABC
Đáp số : Sẽ có một tam giác nhỏ hơn \(\frac{1}{4}\) diện tích tam giác ABC
Sorry bạn na , mk mới lớp 5 chẳng hiểu gì hết