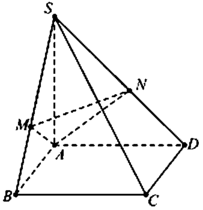
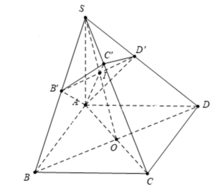
Bài 1 : cho hình chóp S.ABCD, ABCD là hình vuông cạnh a, SA= a căn 2 , SA vuông góc với ABCD. Gọi M,N lần lượg là hình chiếu của A lên SB,SD. CMR: SC vuông góc với (AMN )
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 3 2019
Đáp án B
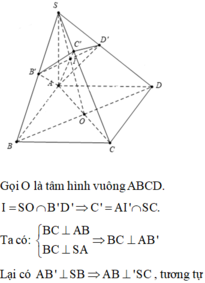
Ta có: B C ⊥ A B B C ⊥ S A ⇒ B C ⊥ M A
Mặt khác A M ⊥ S B ⇒ A M ⊥ S B C ⇒ A N ⊥ S C , tương tự A N ⊥ S C
Do đó S C ⊥ A M N , mặt khác ∆ S B C vuông tại B suy ra tan B S C ^ = B C S B = a S A 2 + A B 2 = 1 3
⇒ S B ; S C ^ = B S C ^ = 30 ° ⇒ S B ; A M N ^ = 60 ° .
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 1
- Đề thiếu dữ liệu liên quan đến điểm S (ví dụ SA hay SB vuông góc đáy gì đó)
- Đề sai (A thuộc SA nên không thể tồn tại M là hình chiếu của A lên SA.)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 3 2023
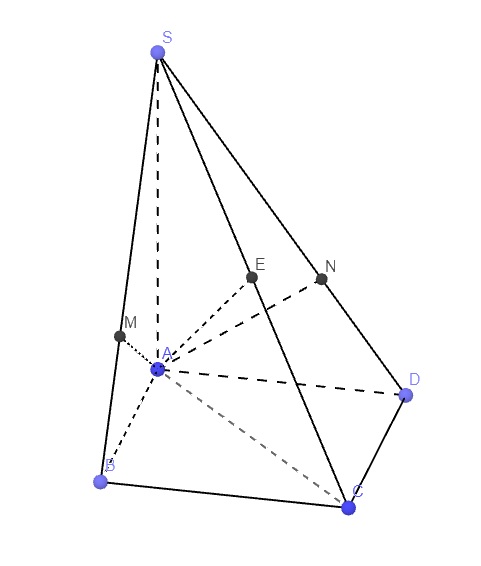
Kẻ AE vuông góc SC (E thuộc SC)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AM\)
\(\Rightarrow AM\perp\left(SBC\right)\Rightarrow AM\perp SC\)
Hoàn toàn tương tự ta có \(AN\perp SC\Rightarrow SC\perp\left(AMN\right)\)
Mà \(AE\perp SC\Rightarrow E\in\left(AMN\right)\)
\(\Rightarrow AE\) là hình chiếu vuông góc của SA lên (AMN)
\(\Rightarrow\widehat{SAE}\) là góc giữa SA và (AMN)
\(AC=a\sqrt{2}\Rightarrow SC=\sqrt{SA^2+AC^2}=2a\)
\(\Delta SAC\) vuông cân tại A \(\Rightarrow AE=SE=\dfrac{1}{2}SC=a\)
\(\Rightarrow\Delta SAE\) vuông cân tại E \(\Rightarrow\widehat{SAE}=45^0\)
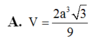
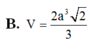
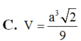
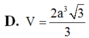
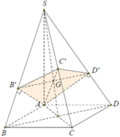
+)CD⊥SA do SA vuông với ABCD
CD⊥AD( tính chất hình vuông)
=>CD⊥(SAD)=>CD⊥AN mà SD⊥AN=> AN⊥(SDC)=>AN⊥SC(1)
+) BC⊥SA do SA vuông với ABCD
BC⊥AB( tính chất hình vuông)
=>BC⊥(SAB)=>BC⊥AM mà SB⊥AM=> AM⊥(SAB)=>AM⊥SC(2)
TỪ 1 và 2 => SC⊥(AMN) đpcm