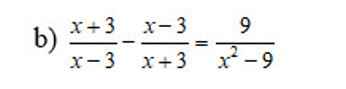
giải giúp pt này vs mn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
V
1
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 9 2021
ĐKXĐ: \(x\ge1\)
\(\sqrt{x-1-4\sqrt{x-1}+4}+\sqrt{x-1-6\sqrt{x-1}+9}=0\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}-2\right)^2}+\sqrt{\left(3-\sqrt{x-1}\right)^2}=0\)
\(\Leftrightarrow\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|=0\)
Do \(\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|\ge\left|\sqrt{x-1}-2+3-\sqrt{x-1}\right|=1>0\) với mọi x thuộc TXĐ
\(\Rightarrow\) Phương trình đã cho vô nghiệm
27 tháng 5 2022
\(\left(x+2\right)\left(\dfrac{360}{x}-6\right)=360\)
\(ĐK:x\ne0\)
\(\Leftrightarrow\left(x+2\right)\left(\dfrac{360-6x}{x}\right)=360\)
\(\Leftrightarrow360-6x+\dfrac{720-12x}{x}=360\)
\(\Leftrightarrow360x-6x^2+720-12x=360x\)
\(\Leftrightarrow6x^2+12x-720=0\)
\(\Delta=12^2-4.6.\left(-720\right)\)
\(=17424>0\)
`->` pt có 2 nghiệm
\(\left\{{}\begin{matrix}x_1=\dfrac{-12-\sqrt{17424}}{12}=-12\\x_2=\dfrac{-12+\sqrt{17424}}{12}=10\end{matrix}\right.\) ( tm )
Vậy \(S=\left\{-12;10\right\}\)
2
27 tháng 5 2022
`48/[x+4]+48/[x-4]=5` `ĐK: x \ne +-4`
`<=>[48(x-4)+48(x+4)]/[(x-4)(x+4)]=[5(x+4)(x-4)]/[(x-4)(x+4)]`
`=>48x-192+48x+192=5x^2-80`
`<=>5x^2-96x-80=0`
`<=>5x^2-100+4x-80=0`
`<=>5x(x-20)+4(x-20)=0`
`<=>(x-20)(5x+4)=0`
`<=>` $\left[\begin{matrix} x=20\\ x=\dfrac{-4}{5}\end{matrix}\right.$ (t/m)
Vậy `S={-4/5;20}`
TC
27 tháng 5 2022
ĐK : \(x\ne\pm4\)
\(\Leftrightarrow\cdot\dfrac{48\left(x+4\right)+48\left(x-4\right)}{\left(x+4\right)\left(x-4\right)}=\dfrac{5\left(x+4\right)\left(x-4\right)}{\left(x+4\right)\left(x-4\right)}\)
\(\Leftrightarrow48x+192+48x-192==5x^2-80\)
\(\Leftrightarrow96x=5x^2-80\)
\(\Leftrightarrow5x^2-96x-80=0\)
\(\Leftrightarrow5x^2+4x-100-80=0\)
\(\Leftrightarrow4\left(x-20\right)+5x\left(x-20\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-20=0\\5x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=20\\x=-\dfrac{4}{5}\end{matrix}\right.\)
NC
0
DH
1
MN
1 tháng 2 2020
HPT : \(\hept{\begin{cases}\frac{1}{x}+\frac{1}{y}=\frac{5}{36}\\\frac{4}{x}+\frac{3}{y}=\frac{1}{2}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\frac{3}{x}+\frac{3}{y}=\frac{5}{12}\left(1\right)\\\frac{4}{x}+\frac{3}{y}=\frac{1}{2}\left(2\right)\end{cases}}\)
Từ (1) và (2), lấy vế trừ vế ta được :
\(\Leftrightarrow\left(\frac{4}{x}+\frac{3}{y}\right)-\left(\frac{3}{x}+\frac{3}{y}\right)=\frac{1}{2}-\frac{5}{12}\)
\(\Leftrightarrow\frac{1}{x}=\frac{1}{12}\)
\(\Leftrightarrow\frac{1}{y}=\frac{5}{36}-\frac{1}{x}=\frac{5}{36}-\frac{1}{12}=\frac{1}{18}\)
\(\Leftrightarrow\hept{\begin{cases}x=12\\y=18\end{cases}}\)
Giải pt . Mn giúp mik vs
4 tháng 8 2023
ĐK: \(-1\le x\le1\)
Đặt \(\sqrt{1-x}=a;\sqrt{x+1}=b\Rightarrow3-x=2a^2+b^2\)
\(pt\Leftrightarrow2a-b+3ab=2a^2+b^2\)
\(\Leftrightarrow2a^2+b^2-2a+b-3ab=0\)
\(\Leftrightarrow2a^2-a\left(3b+2\right)+b^2+b=0\)
\(\Delta=\left(3b+2\right)^2-4.2.\left(b^2+b\right)=9b^2+12b+4-8b^2-8b\)
\(=b^2+4b+4=\left(b+2\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}a=\dfrac{3b+2-\left(b+2\right)}{4}=\dfrac{2b}{4}=\dfrac{b}{2}\Leftrightarrow2a=b\left(1\right)\\a=\dfrac{3b+2+b+2}{4}=\dfrac{4b+4}{4}=b+1\left(2\right)\end{matrix}\right.\)
pt (1) \(\Leftrightarrow2\sqrt{1-x}=\sqrt{x+1}\)
\(\Leftrightarrow4\left(1-x\right)=x+1\)
\(\Leftrightarrow5x=3\Leftrightarrow x=\dfrac{5}{3}\left(tm\right)\)
\(pt\left(2\right)\Leftrightarrow\sqrt{1-x}=1+\sqrt{x+1}\)
\(\Leftrightarrow1-x=1+x+1+2\sqrt{x+1}\)
\(\Leftrightarrow-1-2x=2\sqrt{x+1}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le-\dfrac{1}{2}\\4x^2+4x+1=4x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le-\dfrac{1}{2}\\4x^2=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le-\dfrac{1}{2}\\\left[{}\begin{matrix}x=\dfrac{\sqrt{3}}{2}\left(l\right)\\x=-\dfrac{\sqrt{3}}{2}\left(tm\right)\end{matrix}\right.\end{matrix}\right.\)
Vậy, pt có tập nghiệm là: \(S=\left\{-\dfrac{\sqrt{3}}{2};\dfrac{5}{3}\right\}\)
9 tháng 11 2023
ĐKXĐ: \(x^2+5x+2>=0\)
=>\(\left[{}\begin{matrix}x>=\dfrac{-5+\sqrt{17}}{2}\\x< =\dfrac{-5-\sqrt{17}}{2}\end{matrix}\right.\)
\(\left(x+1\right)\left(x+4\right)-3\sqrt{x^2+5x+2}=6\)
=>\(x^2+5x+4-3\sqrt{x^2+5x+2}-6=0\)
=>\(x^2+5x+2-3\sqrt{x^2+5x+2}-4=0\)(1)
Đặt \(\sqrt{x^2+5x+2}=a\)(a>=0)
Phương trình (1) trở thành:
\(a^2-3a-4=0\)
=>(a-4)(a+1)=0
=>\(\left[{}\begin{matrix}a=4\left(nhận\right)\\a=-1\left(loại\right)\end{matrix}\right.\)
=>\(x^2+5x+2=4^2=16\)
=>\(x^2+5x-14=0\)
=>\(\left(x+7\right)\left(x-2\right)=0\)
=>\(\left[{}\begin{matrix}x=-7\left(nhận\right)\\x=2\left(nhận\right)\end{matrix}\right.\)
QL
1
7 tháng 2 2022
a) \(\left(x+1\right)^4+\left(x+3\right)^4=2m\left(1\right)\)
Đặt \(x+2=t\)
Khi đó phương trình \(\left(1\right)\) trở thành \(\left(t-1\right)^4+\left(t+1\right)^4=2m\)
\(\Leftrightarrow2t^4+12t^2-2m+2=0\)
\(\Leftrightarrow t^4+6t^2-m+1=0\left(2\right)\)
Đặt \(t^2=u\left(u\ge0\right)\)
Khi đó phương trình \(\left(2\right)\) trở thành \(u^2+6u-m+1=0\left(3\right)\)
Thay \(m=1\) vào \(\left(3\right)\) ta có:
\(u^2+6u-1+1=0\Leftrightarrow u^2+6u=0\Leftrightarrow u\left(u+6\right)=0\Leftrightarrow\left[{}\begin{matrix}u=0\\u+6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}u=0\left(\text{nhận}\right)\\y=-6\left(\text{loại}\right)\end{matrix}\right.\)
\(\Rightarrow x+2=0\Leftrightarrow x=-2\)
Vậy với \(m=1\) thì phương trình có nghiệm là \(x=-2\).
b) Để phương trình có hai nghiệm phân biệt thì \(\left(3\right)\) trái dấu \(\Leftrightarrow-m+1< 0\Leftrightarrow m>1\)
Vậy với \(m>1\) thì phương trình có hai nghiệm phân biệt.
\(\dfrac{x+3}{x-3}-\dfrac{x-3}{x+3}=\dfrac{9}{x^2-9}\left(ĐKXĐ:x\ne\pm3\right)\)
\(\Leftrightarrow\dfrac{\left(x+3\right)^2-\left(x-3\right)^2}{\left(x-3\right)\left(x+3\right)}=\dfrac{9}{\left(x-3\right)\left(x+3\right)}\)
\(\Rightarrow x^2+6x+9-x^2+6x-9=9\)
\(\Leftrightarrow12x=9\)
\(\Leftrightarrow x=\dfrac{3}{4}\) (nhận).
Vậy \(S=\left\{\dfrac{3}{4}\right\}\)