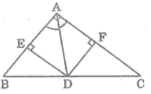
Cho tam giác ABC, đường phân giác AD. Vẽ DE//AB ,DF//AC ( E thuộc AC, F thuộc AB) biết AB = 3cm , AC = 6cm. Hỏi tứ giác AEDF là hình gì và tính chu vi của nó?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
13 tháng 9 2021
Lời giải:
$DF\parallel AE, DE\parallel AF$ nên $AEDF$ là hình bình hành
$P_{AEDF}=AE+DF+DE+AF$
Lại có:
$DF\parallel AC$ nên áp dụng định lý Talet:
$\frac{DF}{AC}=\frac{BF}{AB}$. Mà $AB=AC$ nên $DF=BF$
$DE\parallel AB$ nên áp dụng định lý Talet:
$\frac{CE}{AC}=\frac{DE}{AB}$ mà $AB=AC$ nên $CE=DE$
Do đó:
$P_{AEDF}=AE+BF+CE+AF=(AE+CE)+(BF+AF)=AC+AB=4+4=8$ (cm)
12 tháng 11 2021
Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
mà AD là tia phân giác
nên AEDF là hình vuông
CM
4 tháng 3 2018
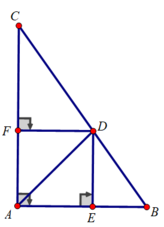
c) Xét tứ giác AEDF có:
∠(EAF) = ∠(AFD) = ∠(AED) = 90 0
⇒ Tứ giác AEDF là hình chữ nhật
Lại có: ΔAFD vuông tại F, có ∠(FAD) = 45 0
⇒ ΔAFD vuông cân tại F
⇒ AF = FD
⇒ tứ giác AEDF là hình vuông
Xét tam giác DEB vuông tại D có:
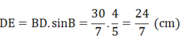
Chu vi hình vuông AEDF là:
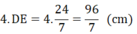
Diện tích hình vuông AEDF là:
CM
7 tháng 4 2017
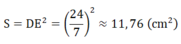
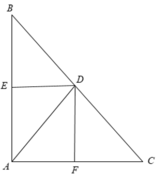
Nên tứ giác AFDE là hình vuông
* Vì DE ⊥ AB, AC ⊥ AB nên DE // AC
Theo định lí Ta-lét ta có: CD/BC = AE/AB
13 tháng 11 2021
Xét tứ giác AEDF có
DE//AF
AE//DF
Do đó: AEDF là hình bình hành
mà \(\widehat{DAE}=90^0\)
nên AEDF là hình chữ nhật
mà AD là tia phân giác
nên AEDF là hình vuông
-Ta có: DE//AB, DF//AC (gt).
\(\Rightarrow\) AEDF là hình bình hành mà AD là tia phân giác của \(\widehat{BAC}\) (gt).
\(\Rightarrow\) AEDF là hình thoi.
-Xét △ABC có: DF//AC (gt).
\(\Rightarrow\dfrac{BF}{AB}=\dfrac{DF}{AC}\) (định lí Ta-let).
\(\Rightarrow1-\dfrac{DF}{AB}=\dfrac{DF}{AC}\)
\(\Rightarrow\dfrac{DF}{AB}+\dfrac{DF}{AC}=1\)
\(\Rightarrow DF.\left(\dfrac{1}{AB}+\dfrac{1}{AC}\right)=1\)
\(\Rightarrow DF.\left(\dfrac{1}{3}+\dfrac{1}{6}\right)=1\)
\(\Rightarrow DF.\dfrac{1}{2}=1\)
\(\Rightarrow DF=2\) (cm).
\(\Rightarrow P_{AEDF}=4.DF=4.2=8\left(cm\right)\) (do AEDF là hình thoi).