Tìm giá trị của x để thõa mãn điều kiện :
1: Cho A = 3 + 32 + 33 + 34 + .... + 3100
Tìm số tự nhiên n biết rằng 2A +3 = 3n
2: Cho M = 3 + 32 + 33 + 34 + ... + 3100
Hỏi :
a) M có chia hết cho 4 , cho 12 không ? vì sao ?
b) Tìm số tự nhiên n biết rằng 2M + 3 = 3n
3: Cho biểu thức : M = 1 + 3 + 32 + 33 +...+ 3118 + 3119
a) Thu gọn biểu thức M
b) Biểu thức M có chia hết cho 5 , cho 13 không ? vì sao?

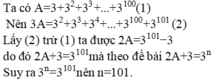
1. Ta có:
3A = 3^2 + 3^3+3^4+...+3^101
=> 3A-A= (3^2+3^3+3^4+...+3^101) - (3+3^2+3^3+...+3^100)
<=> 2A= 3^101-3
=> 2A +3 = 3^101
Mà 2A+3=3^n
=> 3^101 = 3^n => n=101
2. M=3+32+33+34+...+3100
=>3M=32+33+34+35+...+3101
=>3M-M= 3101-3 ( chỗ này bạn tự làm được nhé)
=> M=\(\frac{3^{101}-3}{2}\)
a) Ta co : 3101=(34)25 .3=8125.3
Bạn học đồng dư thức rồi thì xem:
Vì 81 đồng dư với 1 (mod 8) => 8125 đồng dư với 1 (mod 8)=> 8125.3 đồng dư với 1.3=3(mod 8)
=> 8125.3-3 đồng dư với 3-3=0 (mod 8)=> 8125.3-3 chia hết cho 8
=>\(\frac{81^{25}.3-3}{2}\)chia hết cho 4=> M chia hết cho 4 (1)
Ma M=3101-3 chia hết cho 3 (2)
Từ (1) và (2) => M chia hết cho 12
b)\(2\left(\frac{3^{101}-3}{2}\right)+3=3^n\)
=> 3101-3 +3 =3n
=> 3101=3n=> n = 101