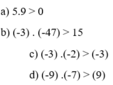A=3/1.5+ 3/5.9+ ......+3/41.45 hãy so sánh A và 117/209
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


D=1/1.5+1/5.9+...+1/41.45
4D=4/1.5+4/5.9+...+4/41.45
4D=1-1/5+1/5-1/9+...+1/41-1/45
4D=1-1/45
D=44/45:4=11/45

\(A=\frac{1}{1.5}+\frac{1}{5.9}+...+\frac{1}{95.99}\)
\(A=\frac{1}{4}.\left(\frac{1}{1}-\frac{1}{5}+...+\frac{1}{95}-\frac{1}{99}\right)\)
\(A=\frac{1}{4}.\left(\frac{1}{1}-\frac{1}{99}\right)\)
\(A=\frac{1}{4}.\frac{98}{99}\)
\(A=\frac{49}{198}\)
Giờ ta so sánh :
\(A=\frac{49}{198}\) và B=1
Ta thấy :
\(\frac{49}{198}<1\)
=> A < B
Vậy A < B

\(\frac{1}{1.5}+\frac{1}{5.9}+\frac{1}{9.13}+\frac{1}{13.17}+...+\frac{1}{41.45}\)
\(=\frac{1}{4}.\left(1-\frac{1}{5}+\frac{1}{5}-\frac{1}{9}+\frac{1}{9}-\frac{1}{13}+...+\frac{1}{41}-\frac{1}{45}\right)\)
\(=\frac{1}{4}.\left(1-\frac{1}{45}\right)\)
\(=\frac{1}{4}.\frac{44}{45}\)
\(=\frac{11}{45}\)
Đặt \(\frac{1}{1\cdot5}+\frac{1}{5\cdot9}+\frac{1}{9\cdot13}+\frac{1}{13\cdot17}+...+\frac{1}{41\cdot45}\) là A.
Ta có:
\(A=\frac{1}{1\cdot5}+\frac{1}{5\cdot9}+\frac{1}{9\cdot13}+\frac{1}{13\cdot17}+...+\frac{1}{41\cdot45}\)
\(4A=4\left(\frac{1}{1\cdot5}+\frac{1}{5\cdot9}+\frac{1}{9\cdot13}+\frac{1}{13\cdot17}+...+\frac{1}{41\cdot45}\right)\)
\(4A=\frac{4}{1\cdot5}+\frac{4}{5\cdot9}+\frac{4}{9\cdot13}+\frac{4}{13\cdot17}+...+\frac{4}{41\cdot45}\)
\(4A=1-\frac{1}{5}+\frac{1}{5}-\frac{1}{9}+\frac{1}{9}-\frac{1}{13}+\frac{1}{13}-\frac{1}{17}+...+\frac{1}{41}-\frac{1}{45}\)
\(4A=1-\frac{1}{45}\)
\(4A=\frac{44}{45}\)
\(A=\frac{44}{45}:4\)
\(A=\frac{11}{45}\)
Vậy \(\frac{1}{1\cdot5}+\frac{1}{5\cdot9}+\frac{1}{9\cdot13}+\frac{1}{13\cdot17}+...+\frac{1}{41\cdot45}=\frac{11}{45}\)

a, \(x-\frac{8}{9}=\frac{1}{3}\)
\(\Leftrightarrow x=\frac{1}{3}+\frac{8}{9}\)
\(\Leftrightarrow x=\frac{11}{9}\)
b, \(\frac{-4}{5}-\frac{8}{15}=\frac{-1}{3}-x\)
\(\Leftrightarrow\frac{-4}{3}=\frac{-1}{3}-x\)
\(\Leftrightarrow x=1\)
c, \(x+\frac{4}{5.9}+\frac{4}{9.13}+...+\frac{4}{41.45}=\frac{-37}{45}\)
Đặt \(A=\frac{4}{5.9}+\frac{4}{9.13}+...+\frac{4}{41.45}\)
\(A=\frac{1}{5}-\frac{1}{9}+\frac{1}{9}-\frac{1}{13}+...+\frac{1}{41}-\frac{1}{45}\)
\(A=\frac{1}{5}-\frac{1}{45}=\frac{8}{45}\)
Thay A vào phép tính
\(\Rightarrow x+\frac{8}{45}=\frac{-37}{45}\)
\(\Rightarrow x=-1\)

\(x+\frac{3}{5.9}+\frac{3}{9.13}+\frac{3}{13.17}+...+\frac{4}{41.45}=-\frac{37}{45}\)
\(\Leftrightarrow x+3\left(\frac{1}{5.9}+\frac{1}{9.13}+\frac{1}{13.17}+...+\frac{1}{41.45}\right)=-\frac{37}{45}\)
\(\Leftrightarrow x+\frac{3}{4}\left(\frac{1}{5}-\frac{1}{9}+\frac{1}{9}-\frac{1}{13}+\frac{1}{13}-\frac{1}{17}+...+\frac{1}{41}-\frac{1}{45}\right)=-\frac{37}{45}\)
\(\Leftrightarrow x+\frac{3}{4}\left(\frac{1}{5}-\frac{1}{45}\right)=-\frac{37}{45}\)
\(\Leftrightarrow x+\frac{3}{4}.\frac{8}{45}=-\frac{37}{45}\)
\(\Leftrightarrow x+\frac{2}{15}=-\frac{37}{45}\)
\(\Leftrightarrow x=-\frac{43}{45}\)

a) A = 4/5.9 + 4/9.13 + 4/13.17 + ... + 4/41/45
A = 1/5 - 1/9 + 1/9 - 1/13 + 1/13 - 1/17 + ... + 1/41 - 1/45
A = 1/5 - 1/45
A = 8/45
b) B = ( 1 - 1/2 ) . ( 1 - 1/3 ) . ( 1 - 1/4 ) . ..... . ( 1 - 1/100 )
B = 1/2 . 2/3 . 3/4 . .... . 99/100
B = \(\frac{1.2.3.......99}{2.3.4......100}\)
B = 1/100
B = \(\left(1-\frac{1}{2}\right)+\left(1-\frac{1}{3}\right)+...+\left(1-\frac{1}{100}\right)\)
B = \(\frac{1}{2}.\frac{2}{3}.....\frac{99}{100}\)
B = \(\frac{1}{100}\)

a) 5.9 > 0
b) (-3) . (-47) > 15
c) (-3) .(-2) > (-3)
d) (-9) .(-7) > (9)