Cho tam giác ABC có cạnh AB < AC. Các đường cao AD và BE của tam giác ABC cắt nhau tại H. Gọi I đối xứng với H qua D. Gọi M và N lần lượt là hình chiếu vuông góc của I trên AB và AC.
a) Chứng minh tứ giác ABDE nội tiếp và góc \(\widehat{CAD}=\widehat{CBI}\) ?
b) Chứng minh rằng góc \(\widehat{MDI}=\widehat{ACI}\) và tam giác ACI đồng dạng với tam giác MDI ?
c) Gọi P và Q lần lượt là trung điểm của MD và AC. Chứng minh rằng góc \(\widehat{IPQ}=90^0\) ?
P/s: Nhờ thầy cô và các bạn giúp đỡ ý c với ạ, cám ơn nhiều ạ!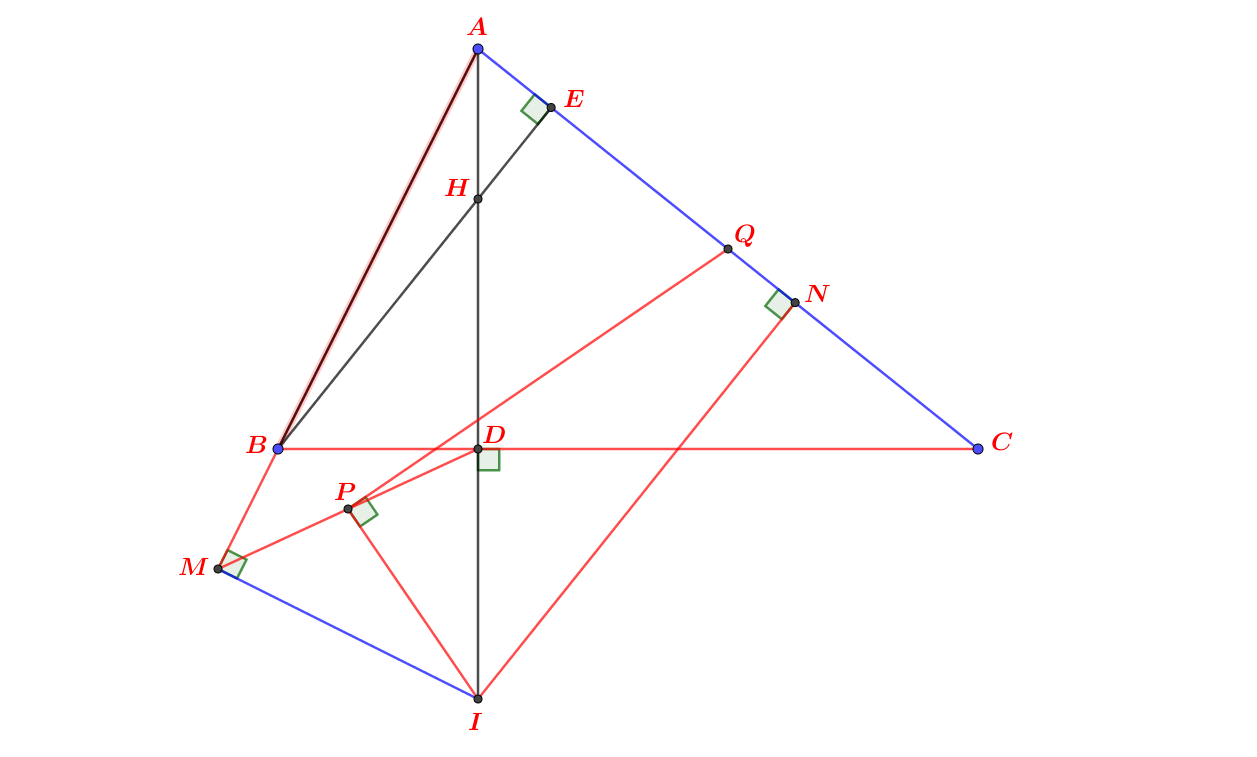
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cạnh BC dài là
12 nhân 5/4 =15
cạnh AC dài là
15-2= 13
Vậy chu vi tam giác ABC là
12+15+13=40 cm

Bài 1:
a: AB+AC=75-45=30(cm)
b: AB=(30+4):2=17(cm)
=>AC=13cm
\(S=17\cdot13=221\left(cm^2\right)\)
Bài 2:
a: BC=67-47=20(cm)
b: \(S=\dfrac{15\cdot20}{2}=15\cdot10=150\left(cm^2\right)\)

bài 2:
ta có: AB<AC<BC(Vì 3cm<4cm<5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
bài 2:
ta có: AB <AC <BC (Vì 3cm <4cm <5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
HT mik làm giống bạn Dương Mạnh Quyết

Câu hỏi của Anh Nguyễn Bảo - Toán lớp 5 - Học toán với OnlineMath
Em xem link ở đây nhé! Bạn @đẹp trai...@ làm đúng rồi đấy
