trình bày chi tiết giúp tôi với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\dfrac{31\cdot\left(31^{12}-1\right)}{31\left(31^{13}+1\right)}=\dfrac{31^{13}+1-32}{31\left(31^{13}+1\right)}=\dfrac{1}{31}-\dfrac{32}{31^{14}+31}\)
\(B=\dfrac{31\left(31^{13}-1\right)}{31\left(31^{14}+1\right)}=\dfrac{1}{31}-\dfrac{32}{31^{15}+31}\)
Dễ thấy \(31^{14}+31< 31^{15}+31\Rightarrow\dfrac{32}{31^{14}+31}>\dfrac{32}{31^{15}+31}\\ \Rightarrow\dfrac{1}{31}-\dfrac{32}{31^{14}+31}< \dfrac{1}{31}-\dfrac{32}{31^{15}+31}\)
Vậy A < B

Bài 6:
Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành


Khối lượng lúa thu được là:
\(150\cdot50:100\cdot80=6000\left(kg\right)=60\left(tạ\right)\)

\(\dfrac{x-1}{3}=\dfrac{2-x}{-2}\)
⇔ \(\dfrac{x-1}{3}=\dfrac{x-2}{2}\)
⇔ \(3x-6-2x+2=0\)
⇔ \(x-4=0\)
⇒ \(x=4\)

d nhận \(\overrightarrow{u}=\left(1;-1;2\right)\) là 1 vtcp và (P) nhận \(\overrightarrow{n}=\left(1;2;-2\right)\) là 1 vtpt
Ta có: \(\overrightarrow{a}=\left[\overrightarrow{u};\overrightarrow{n}\right]=\left(-2;4;3\right)\)
\(\Rightarrow\left[\overrightarrow{a};\overrightarrow{n}\right]=\left(-14;-1;-8\right)=-1\left(14;1;8\right)\)
Phương trình d dạng tham số: \(\left\{{}\begin{matrix}x=t\\y=-t\\z=2t+1\end{matrix}\right.\)
Gọi M là giao điểm d và (P), tọa độ M thỏa:
\(t+2\left(-t\right)-2\left(2t+1\right)+2=0\Rightarrow t=0\Rightarrow M\left(0;0;1\right)\)
Hình chiếu vuông góc của d lên (P) nhân (14;1;8) là 1 vtpt và đi qua M nên có dạng:
\(\dfrac{x}{14}=\dfrac{y}{1}=\dfrac{z-1}{8}\)


Câu 1:
\(\left\{{}\begin{matrix}y-2x< =2\\2y-x>=4\\x+y< =5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y< =2x+2\\2y>=x+4\\y< =-x+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y< =2x+2\\y< =-x+5\\y>=\dfrac{1}{2}x+2\end{matrix}\right.\)
y<=2x+2
=>y-2x-2<=0
Vẽ đường thẳng y=2x+2
Khi x=0 và y=0 thì \(y-2x-2=0-0-2=-2< =0\)(đúng)
=>Miền nghiệm của BPT y<=2x+2 là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0)
y<=-x+5
=>x+y-5<=0
Khi x=0 và y=0 thì \(x+y-5=0+0-5< =0\)(đúng)
=>Miền nghiệm của BPT y<=-x+5 là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0)
y>=1/2x+2
=>\(-\dfrac{1}{2}x+y-2>=0\)
Khi x=0 và y=0 thì \(-\dfrac{1}{2}x+y-2=-\dfrac{1}{2}\cdot0+0-2=-2< 0\)
=>O(0;0) không thỏa mãn BPT \(-\dfrac{1}{2}x+y-2>=0\)
=>Miền nghiệm của BPT \(y>=\dfrac{1}{2}x+2\) là nửa mặt phẳng chứa biên nhưng không chứa điểm O(0;0)
Vẽ đồ thị:
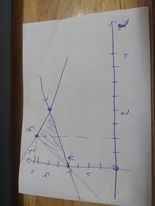
Theo hình vẽ, ta có: Miền nghiệm của hệ BPT sẽ là ΔABC, với A(0;2); B(1;4); C(2;3)
Khi x=0 và y=2 thì F=2-0=2
Khi x=1 và y=4 thì F=4-1=3
Khi x=2 và y=3 thì F=3-2=1
=>Chọn A



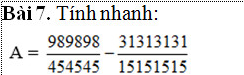

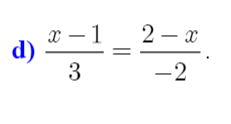



\(\Leftrightarrow2x-\dfrac{1}{2}=\dfrac{-17}{20}\cdot\dfrac{5}{17}=\dfrac{-1}{4}\)
=>2x=1/2-1/4=1/4
hay x=1/8
\(\Leftrightarrow2x-\dfrac{1}{2}=-\dfrac{1}{4}\Leftrightarrow2x=\dfrac{1}{4}\Leftrightarrow x=\dfrac{1}{8}\)