Bài 1. Một canô xuôi dòng từ bến sông A đến bến sông B cách nhau 24 km; cùng lúc đó, cũng từ A về B một bè nứa trôi với vận tốc dòng nước là 4 km/h. Khi đến B canô quay lại ngay và gặp bè nứa tại địa điểm C cách A là 8 km. Tính vận tốc thực của canô. lập hệ phương trình

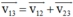 (0,25 đ)
(0,25 đ)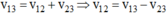 (0,50 đ)
(0,50 đ)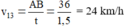 (0,25đ)
(0,25đ)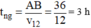 (0,25đ)
(0,25đ)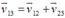 (0,25 điểm)
(0,25 điểm)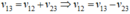 (0,25 điểm)
(0,25 điểm)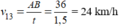 (0,25 điểm)
(0,25 điểm)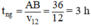 (0,25 điểm)
(0,25 điểm)
Gọi vận tốc thực của ca nô là: x (km/h)
=> vận tốc cano xuôi dòng và ngược dòng là: x+4; x-4 (km/h)
Do ca nô gặp bè nứa tại điểm cách A là 8km nên nó ngược dòng từ B được 24-8=16 km thì gặp bè
Thời gian ca nô xuôi và ngược dòng là: 24x+4+16x−4(h)24x+4+16x−4(h)
+ Do bè nứa trôi 8km với vận tốc dòng nước nên nó trôi trong: 8/4=2 (h)
Ta có:
\(\dfrac{24}{x+4}\)+\(\dfrac{16}{x-4}\)= 2
=> \(\dfrac{12\left(x-4\right)+8\left(x+4\right)}{\left(x-4\right)\left(x+4\right)}\)= 1
=> 12x - 48 + 8x + 32 = \(^{x^2}\)- 16
=>\(^{x^2}\)- 20x = 0
=> x = 20 ( km / h ) ( do : x > 0 )
vậy vận tốc là 20 ( km /h )
thời gian cano xuôi và ngược dòng là : \(\dfrac{24}{x+4}\)+ \(\dfrac{16}{x-4}\)