Bài 4.Cho tam giác ABC vuông tại A, kẻ đường phân giác BI (I thuộc AC) , kẻ ID vuông góc với BC (D thuộc BC). a) Chứng minh tam giác AIB = tam giác DIB
b) Chứng minh BI vuông góc AD
c) Gọi E là giao điểm của BA và DI. Chứng minh AD// EC
d) Chứng minh EIC cân

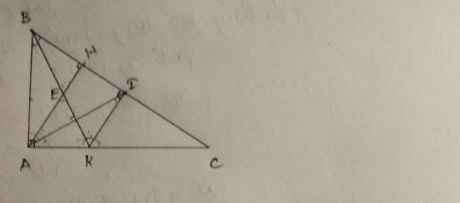
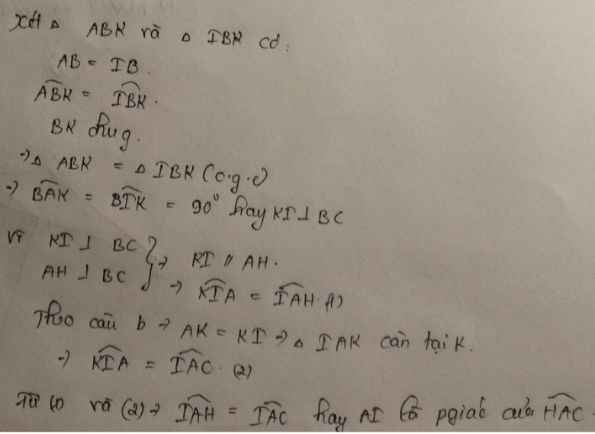
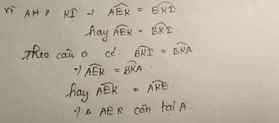
a: Xét ΔAIB vuông tại A và ΔDIB vuông tại D có
IB chung
\(\widehat{ABI}=\widehat{DBI}\)
Do đó: ΔAIB=ΔDIB
b: Ta có: ΔAIB=ΔDIB
nên AI=DI; BA=BD
Ta có: IA=ID
nên I nằm trên đường trung trực của AD(1)
Ta có: BA=BD
nên B nằm trên dường trung trực của AD(2)
Từ (1) và (2) suy ra BI⊥AD
c:Xét ΔAIE vuông tại A và ΔDIC vuông tại D có
IA=ID
\(\widehat{AIE}=\widehat{DIC}\)
Do đó: ΔAIE=ΔDIC
Suy ra: AE=DC
Xét ΔBEC có
BA/AE=BD/DC
nên AD//EC
d: Xét ΔIEC có IE=IC
nên ΔIEC cân tại I