giúp em bài 6,7,8 với ạ, em cần gấp 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số sản phẩm àm 2 ng công nhân được giao là x (x∈N*, sản phẩm)
Thời gian hoàn thành công việc của người thứ nhất là: \(\dfrac{x}{40}\left(h\right)\)
Thời gian hoàn thành công việc của ngươi thứ hai là: \(\dfrac{x}{50}\left(h\right)\)
Vì ng thứ nhất hoàn thành công việc chậm hơn người thứ hai 2 giờ nên ta có PT:
\(\dfrac{x}{40}-\dfrac{x}{50}=2\)
⇔\(50x-40x=4000\)
⇔\(10x=4000\)
⇔\(x=400\)
Vậy số sản phẩm mỗi công nhân được giao là 400 (sản phẩm)

lần đổ 1
\(\left(mC+m'C'\right).\left(38-20\right)=mC.\left(60-38\right)\)
\(\Leftrightarrow\left(mC+m'C'\right)18=mC.22\)
\(\Leftrightarrow2mC=9m'C'\)
lần 2 \(\left(2mC+m'C'\right)\left(t_x-38\right)=mC.\left(60-t_x\right)\)
\(11m'C'\left(t_x-38\right)=\dfrac{9}{2}.m'C'\left(60-t_x\right)\)
\(\Rightarrow t_x=...\)

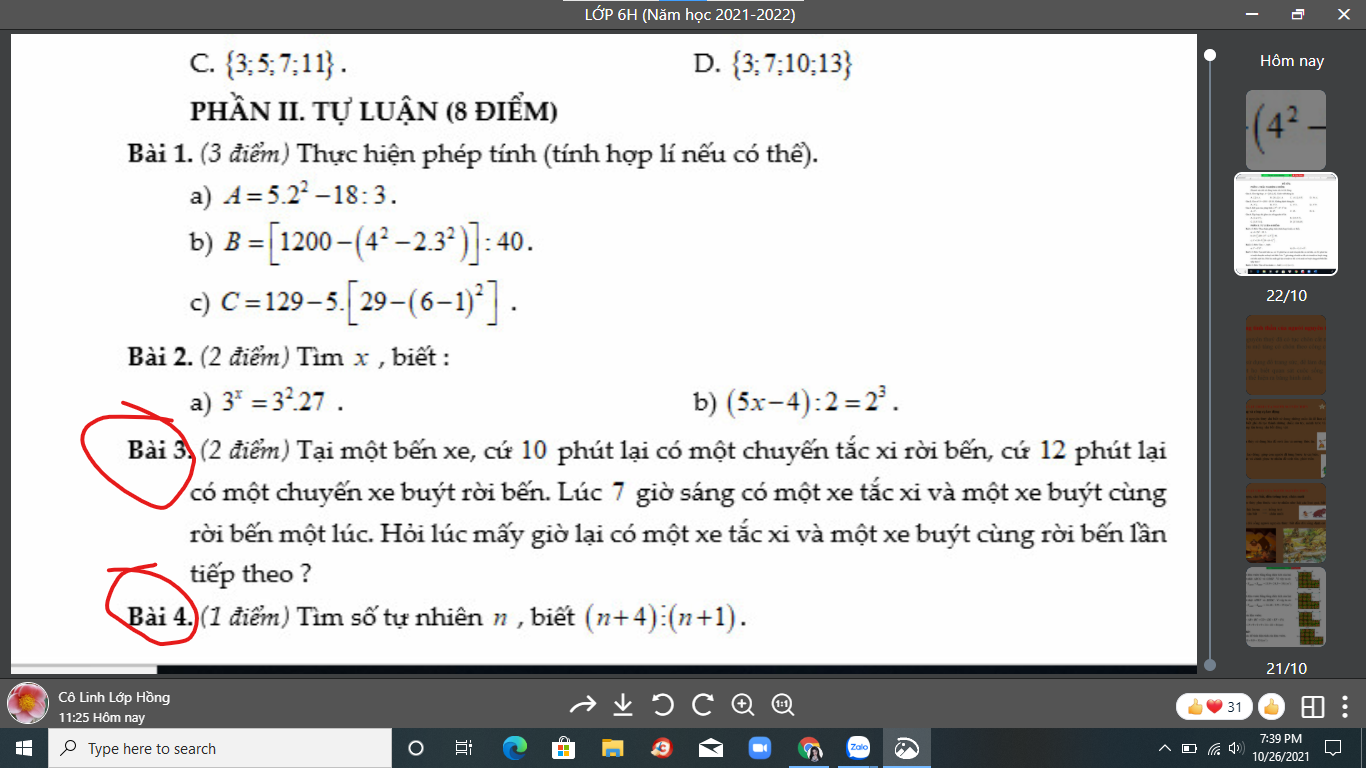
Bài 4:
\(\Leftrightarrow n+1\in\left\{1;3\right\}\)
hay \(n\in\left\{0;2\right\}\)
\(\left(n+4\right)⋮\left(n+1\right)\Rightarrow\left(n+1\right)+3⋮\left(n+1\right)\)
\(\Rightarrow\left(n+1\right)\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)
Mà \(n\in N\)
\(\Rightarrow n\in\left\{0;2\right\}\)


6:
\(2^{225}=\left(2^3\right)^{75}=8^{75}\)
\(3^{150}=\left(3^2\right)^{75}=9^{75}\)
mà 8<9
nên \(2^{225}< 3^{150}\)
4: \(\left|5x+3\right|>=0\forall x\)
=>\(-\left|5x+3\right|< =0\forall x\)
=>\(-\left|5x+3\right|+5< =5\forall x\)
Dấu = xảy ra khi 5x+3=0
=>x=-3/5
1:
\(\left(2x+1\right)^4>=0\)
=>\(\left(2x+1\right)^4+2>=2\)
=>\(M=\dfrac{3}{\left(2x+1\right)^4+2}< =\dfrac{3}{2}\)
Dấu = xảy ra khi 2x+1=0
=>x=-1/2


bn chụp màn hình sao vậy? k bt giống bn k alt+ctrl+a
Bài 5:
a: \(x\left(x-1\right)-x^2+4x=-3\)
\(\Leftrightarrow x^2-x-x^2+4x=-3\)
hay x=-1
b: \(6x^2-\left(2x+5\right)\left(3x-2\right)=7\)
\(\Leftrightarrow6x^2-6x^2+4x-15x+10=7\)
\(\Leftrightarrow-11x=-3\)
hay \(x=\dfrac{3}{11}\)
 em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp
em cần giải gấp bài 3 chi tiết mọi người giúp em với ạ. Làm bài dưới dạng phân số ạ em cần gấp

 giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ
giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ Ạ,GIÚP EM VỚI Ạ
Ạ,GIÚP EM VỚI Ạ
 giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
Bài 6:
\(\dfrac{x-1}{2013}+\dfrac{x-2}{2012}+\dfrac{x-3}{2011}=\dfrac{x-4}{2010}+\dfrac{x-5}{2009}+\dfrac{x-6}{2008}\)
⇔\(\dfrac{x-1}{2013}-1+\dfrac{x-2}{2012}-1+\dfrac{x-3}{2011}-1=\dfrac{x-4}{2010}-1+\dfrac{x-5}{2009}-1+\dfrac{x-6}{2008}-1\)⇔\(\dfrac{x-2014}{2013}+\dfrac{x-2014}{2012}+\dfrac{x-2014}{2011}=\dfrac{x-2014}{2010}+\dfrac{x-2014}{2009}+\dfrac{x-2014}{2008}\)
⇔\(\dfrac{x-2014}{2013}+\dfrac{x-2014}{2012}+\dfrac{x-2014}{2011}-\dfrac{x-2014}{2010}-\dfrac{x-2014}{2009}-\dfrac{x-2014}{2008}=0\)
⇔\(\left(x-2014\right)\left(\dfrac{1}{2013}+\dfrac{1}{2012}+\dfrac{1}{2011}-\dfrac{1}{2010}-\dfrac{1}{2009}-\dfrac{1}{2008}\right)=0\)
Vì \(\dfrac{1}{2013}+\dfrac{1}{2012}+\dfrac{1}{2011}-\dfrac{1}{2010}-\dfrac{1}{2009}-\dfrac{1}{2008}\ne0\)
\(\Rightarrow x-2014=0\)
⇔\(x=2014\).
-Vậy \(S=\left\{2014\right\}\).
Bài 7:
\(x^2-4x+y^2-6y+15=2\)
⇔\(x^2-4x+y^2-6y+15-2=0\)
⇔\(x^2-4x+y^2-6y+13=0\)
⇔\(\left(x^2-4x+4\right)+\left(y^2-6y+9\right)=0\)
⇔\(\left(x-2\right)^2+\left(y-3\right)^2=0\)
Vì \(\left(x-2\right)^2\ge0,\left(y-3\right)^2\ge0\).
\(\Rightarrow\)\(\left(x-2\right)^2=0\) và \(\left(y-3\right)^2=0\)
⇔\(x=2\) và \(y=3\).
Bài 8:
\(\left(x^2+1\right)^2+3x\left(x^2+1\right)+2x^2=0\)
⇔\(\left(x^2+1\right)^2+2x\left(x^2+1\right)+x^2+x\left(x^2+1\right)+x^2=0\)
⇔\(\left(x^2+1+x\right)^2+x\left(x^2+1+x\right)=0\)
⇔\(\left(x^2+1+x\right)\left(x^2+1+x+x\right)=0\)
⇔\(x^2+x+1=0\) (vô nghiệm, bạn tự c/m) hay \(x^2+2x+1=0\)
⇔\(x^2+2x+1=0\)
⇔\(\left(x+1\right)^2=0\)
⇔\(x=-1\).
-Vậy \(S=\left\{-1\right\}\)