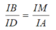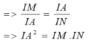Cho hình bình hành ABCD có AB=8cm, AD=6cm. Trên cạnh BC lấy M sao cho BM= 4cm. Đường thẳng AM cắt đường chéo BD tại I, cắt đường thẳng DC tại N.
a) Chứng minh tam giác MAB đồng dạng tam giác AND
b) Tính độ dài DN và CN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ (1) // CD AB // ND
(5)
Từ (1) (2 góc đối của hình bình hành) (6)
Từ (5), (6) (G-G)

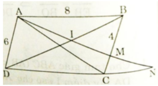
a) AD // BC (gt)![]()
b) Xét ΔAMB và ΔNAD có:
∠BAM = ∠ AND (so le trong, AB // CD)
∠ABM = ∠ADN (góc đối của hình bình hành)
⇒ ΔAMB ∼ ΔNAD (g.g)
c) ΔAMB ∼ ΔNAD (cmt)
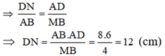
Do đó: CN = DN – DC = 12 – 8 = 4 (cm)
d) Do AB //CD nên theo hệ quả định lí Ta-lét, ta có
![]()
Tương tự, do AD // BM nên