Tìm hai số biết rằng tổng của chúng bằng 3 ; lấy số lớn chia cho số bé cũng được thương là 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 12 2014
a) n=7k+1 ( \(k\in N\))
b) 18 va 66 hoac 6 va 78 hoac 30 va 54
c) 15 va 20 hoac 5 va 60
d) 10 va 900 hoac 20 va 450 hoac 180 va 50 hoac 100 va 90
13 tháng 12 2016
a, Gọi hai số tự nhiên cần tìm là a và b
Ta có : \(a=6.k_1;b=6.k_2\)
Trong đó : \(ƯCLN\left(k_1,k_2\right)=1\)
Mà : \(a+b=84\Rightarrow6.k_1+6.k_2=84\)
\(\Rightarrow6\left(k_1+k_2\right)=84\Rightarrow k_1+k_2=84\div6=14\)
+) Nếu : \(k_1=1\Rightarrow k_2=13\Rightarrow\begin{cases}a=6\\b=78\end{cases}\)
+)Nếu : \(k_1=3\Rightarrow k_2=11\Rightarrow\begin{cases}a=18\\b=66\end{cases}\)
+)Nếu : \(k_1=5\Rightarrow k_2=9\Rightarrow\begin{cases}a=30\\b=54\end{cases}\)
Vậy ...
b, Tương tự câu a,
c, Gọi hai số tự nhiên cần tìm là a và b
Vì : \(ƯCLN\left(a,b\right)=10;BCNN\left(a,b\right)=900\)
\(\RightarrowƯCLN\left(a,b\right).BCNN\left(a,b\right)=a.b=900.10=9000\)
Phần còn lại giống câu a và câu b tự làm
10 tháng 12 2023
Bài 1:
Gọi hai số tự nhiên cần tìm là a,b
Số thứ nhất gấp 4 lần số thứ hai nên a=4b(1)
Tổng của hai số là 100 nên a+b=100(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}a=4b\\a+b=100\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4b+b=100\\a=4b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5b=100\\a=4b\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=\dfrac{100}{5}=20\\a=4\cdot20=80\end{matrix}\right.\)
Bài 2:
Gọi hai số cần tìm là a,b
Hiệu của hai số là 10 nên a-b=10(4)
Hai lần số thứ nhất bằng ba lần số thứ hai nên 2a=3b(3)
Từ (3) và (4) ta có hệ phương trình:
\(\left\{{}\begin{matrix}a-b=10\\2a=3b\end{matrix}\right.\Leftrightarrow\)\(\left\{{}\begin{matrix}a-b=10\\2a-3b=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a-2b=20\\2a-3b=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a-2b-2a+3b=20\\2a=3b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=20\\2a=3\cdot20=60\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=30\\b=20\end{matrix}\right.\)
Bài 3:
Gọi số tự nhiên cần tìm có dạng là \(\overline{ab}\left(a\ne0\right)\)
Chữ số hàng chục bé hơn chữ số hàng đơn vị là 3 nên b-a=3(5)
Nếu đổi chỗ hai chữ số cho nhau thì tổng của số mới lập ra và số ban đầu là 77 nên ta có:
\(\overline{ab}+\overline{ba}=77\)
=>\(10a+b+10b+a=77\)
=>11a+11b=77
=>a+b=7(6)
Từ (5) và (6) ta có hệ phương trình:
\(\left\{{}\begin{matrix}-a+b=5\\a+b=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-a+b+a+b=5+7\\a+b=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2b=12\\a+b=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=6\\a=7-6=1\end{matrix}\right.\)
Vậy: Số tự nhiên cần tìm là 16
19 tháng 7 2016
1) Bài giải :
Đáp số : Sai đề , vì tổng của 3 số lẻ là số lẻ .
2) Bài giải :
Số thứ hai là :
\(2028\div3=676\)
Ba số chẵn liên tiếp có hiệu là 2 .
Vậy số thứ nhất là :
\(676-2=674\)
Số thứ ba là :
\(676+2=678\)
_ Vậy 3 số chẵn liên tiếp đó là : \(674,676,678.\)
Đáp số : Số chẵn thứ nhất : \(674.\)
Số chẵn thứ hai : \(676.\)
Số chẵn thứ ba : \(678.\)
PT
1
CM
26 tháng 4 2017
Vì hai số có tổng bằng 10 và tích bằng -10 nên nó là nghiệm của phương trình: x 2 – 10x – 10 = 0
Ta có: ∆ ' = - 5 2 – 1.(-10) = 25 + 10 = 35 > 0
∆ ' = 35
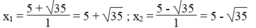
Vậy hai số đó là 5 + 35 và 5 - 35
VP
0
NH
0
BP
3
9 tháng 1 2022
Số thứ nhất là:
\(58.1\cdot\dfrac{3}{7}=24,9\)
Số thứ hai là:
58,1-24,9=33,2
9 tháng 1 2022
Số lớn là:
\(\left(58,1+0,75\right):2=29,425\)
Số bé là:
\(58,1-29,425=28,675\)