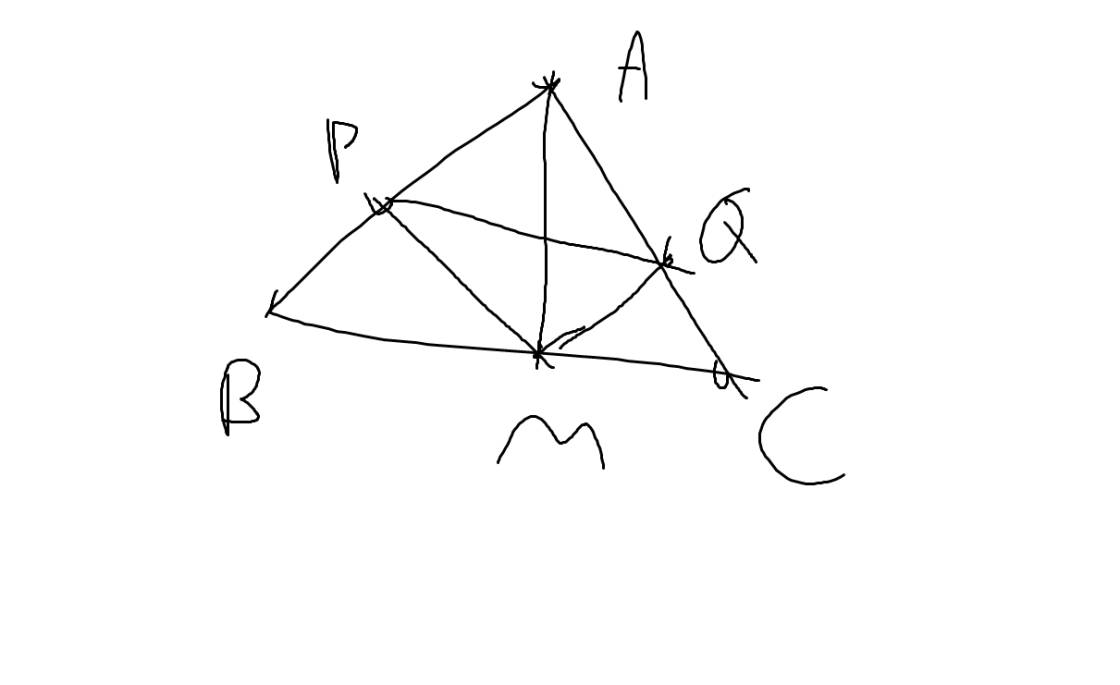
cho tam giác ABC (hình vẽ) có AM=MP=PB; AN=NQ=QC.
A) tìm trên hình vẽ những tam giác có diện tích bằng nhau .giải thích tại sao ?
b)biết diện tích tam giác AMN =5cm vuông .tính diện tích tứ giác MNPQ và diện tích tam giác ABC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Diện h tam giác ABC là :
7,2 x 7,5 : 2 = 27 ( cm2 )
b) Nối P với C
Xét hai tam giác APC và ABC
Chung chiều cao hạ từ đỉnh C xuống cạnh AB
PA = 2/3 AB
=> SAPC = SABC x 2/3 = 27 x 2/3 = 18 ( cm2 )
Xét 2 tam giác APQ và APC
Chung chiều cao hạ từ đỉnh P xuống cạnh AC
AQ = 1/4 AC
=> SAPQ = SAPC X 1/4 = 18 x 1/4 = 4,5 ( cm2 )
Đáp số : 4,5 cm2
bn wiiiiiiiii có đúng ko zậy
a) Diện h tam giác ABC là :
7,2 x 7,5 : 2 = 27 ( cm2 )
b) Nối P với C
Xét hai tam giác APC và ABC
Chung chiều cao hạ từ đỉnh C xuống cạnh AB
PA = 2/3 AB
=> SAPC = SABC x 2/3 = 27 x 2/3 = 18 ( cm2 )
Xét 2 tam giác APQ và APC
Chung chiều cao hạ từ đỉnh P xuống cạnh AC
AQ = 1/4 AC
=> SAPQ = SAPC X 1/4 = 18 x 1/4 = 4,5 ( cm2 )
Đáp số : 4,5 cm2

Sửa đề: MN-NP=3cm
ΔABC=ΔMNP
=>AB=MN; BC=NP; AC=MP
MN-NP=3
=>AB-BC=3
mà AB+BC=7
nên \(AB=\dfrac{3+7}{2}=5cm;BC=AB-3=5-3=2cm\)
MP=AC
mà MP=4cm
nên AC=4cm
Chu vi tam giác ABC là:
\(C_{ABC}=AB+AC+BC=5+4+2=11\left(cm\right)\)
Chu vi tam giác MNP là:
\(C_{MNP}=MN+NP+MP=5+4+2=11\left(cm\right)\)

a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔPAM vuông tại P và ΔQAM vuông tại Q có
AM chung
\(\widehat{PAM}=\widehat{QAM}\)
Do đó: ΔPAM=ΔQAM
=>PA=QA và MP=MQ
b: AP=AQ
=>A nằm trên đường trung trực của PQ(1)
MP=MQ
=>M nằm trên đường trung trực của PQ(2)
Từ (1) và (2) suy ra AM là đường trung trực của PQ
=>AM\(\perp\)PQ

a: Xét ΔNMA và ΔNPB có
NM=NP
\(\widehat{NMA}=\widehat{NPB}\)
MA=PB
Do đó: ΔNMA=ΔNPB
Suy ra: NA=NB
hay ΔNAB cân tại N
b: Xét ΔNHM vuông tại H và ΔNKP vuông tại K có
NM=NP
\(\widehat{HNM}=\widehat{KNP}\)
Do đó: ΔNHM=ΔNKP
Suy ra: MH=PK

b,- Ta có : AM là đường trung tuyến của tam giác vuông ABC .
=> AM = BM = CM = KM .
Xét \(\Delta MKC\) và \(\Delta MAB\) có :
\(\left\{{}\begin{matrix}BM=MC\\AM=MK\\\widehat{BMA}=\widehat{KMC}\end{matrix}\right.\)
=> \(\Delta MKC\) = \(\Delta MAB\) ( c - g - c )
- Xét tứ giác ABKC có :
AM = BM = CM = KM và tam giác ABC vuông tại A .
=> Tứ giác ABKC là hình chữ nhật.
=> KC vuông góc với AC .
c, - Áp dụng định lý pitago vào tam giác ABC vuông tại A :
\(BC=\sqrt{AB^2+AC^2}=13\left(cm\right)\)
Ta có : \(AM=\dfrac{1}{2}BC=\dfrac{13}{2}\)

A B C M
ta có: AM = 1/2 BC => AM = BM, CM
xét tam giác ABM có : AM = BM
=> ABM cân tại M
xét tam giác ACM có : AM = CM
=> ACM cân tại M
Mà góc AMB + AMC = 180 độ ( kề bù )
=> góc B + góc BAM + góc C + góc CAM = 180 độ
Mà góc B = góc BAM
góc C = góc CAM
=> BAM + CAM = 90 độ
=> tam giác ABC cân tại A
mk bk làm nè
neu ai giai duoc cho minh bai nay thi minh se ve so do va nho cac cau giai ho