Giúp em làm với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LK
giúp em với ạ em đang cần gấp ạ. Bài nào làm đc trc thì làm trc giúp em với ạ
1
28 tháng 10 2023
6:
\(2^{225}=\left(2^3\right)^{75}=8^{75}\)
\(3^{150}=\left(3^2\right)^{75}=9^{75}\)
mà 8<9
nên \(2^{225}< 3^{150}\)
4: \(\left|5x+3\right|>=0\forall x\)
=>\(-\left|5x+3\right|< =0\forall x\)
=>\(-\left|5x+3\right|+5< =5\forall x\)
Dấu = xảy ra khi 5x+3=0
=>x=-3/5
1:
\(\left(2x+1\right)^4>=0\)
=>\(\left(2x+1\right)^4+2>=2\)
=>\(M=\dfrac{3}{\left(2x+1\right)^4+2}< =\dfrac{3}{2}\)
Dấu = xảy ra khi 2x+1=0
=>x=-1/2
14 tháng 4 2022
Bài 3:
Số học sinh kém là:
40-8-10-20=2(bạn)
Tỉ số phần trăm giữa số học sinh giỏi so với lớp là:
8:40=20%
Tỉ số phần trăm giữa số học sinh khá so với lớp là:
20:40=50%
Tỉ số phần trăm giữa số học sinh trung bình so với lớp là:
10:40=25%
Tỉ số phần trăm giữa số học sinh yếu so với lớp là:
2:40=5%
KM
0
D
2
NA
10 tháng 3 2022
bài 3:
tổng số giờ đã chảy đc từ 2 vòi : 1+1=2(giờ)
tổng số phần bể đã chảy được từ 2 vòi : \(\dfrac{1}{5}+\dfrac{1}{7}=\dfrac{7}{35}+\dfrac{5}{35}=\dfrac{12}{35}\left(ph\text{ần} b\text{ể}\right)\)
nếu chảy cùng lúc mỗi giờ chảy được : \(\dfrac{12}{35}:2=\dfrac{12}{35\cdot2}=\dfrac{6}{35}\left(ph\text{ần}b\text{ể}\right)\)
bài 4:
cách 1:
độ dài đoạn AB là : \(\dfrac{3}{4}+\dfrac{9}{8}=\dfrac{18}{24}+\dfrac{27}{24}=\dfrac{45}{24}\left(m\right)\)
diện tích ABCD là : \(\dfrac{45}{27}\cdot\dfrac{4}{7}=\dfrac{15}{14}\left(m^2\right)\)
cách 2:
diện tích AEFD là : \(\dfrac{3}{4}\cdot\dfrac{4}{7}=\dfrac{3}{7}\left(m^2\right)\)
diện tích EBCF là : \(\dfrac{9}{8}\cdot\dfrac{4}{7}=\dfrac{9}{14}\left(m^2\right)\)
diện tích ABCD là : \(\dfrac{3}{7}+\dfrac{9}{14}=\dfrac{15}{14}\left(m^2\right)\)
T
1
2 tháng 1 2022
a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM⊥AB
A
16 tháng 11 2021
Công thức đây nhé (Áp dụng làm thử đi)
Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α\alphaα, kí hiệu sinα\sin\alphasinα.Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc α\alphaα, kí hiệu cosα\cos\alphacosα.
Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc α\alphaα, kí hiệu tanα\tan\alphatanα.
Tỉ số giữa cạnh kề và cạnh đối gọi là côtang của góc α\alphaα, kí hiệu cotα\cot\alphacotα.
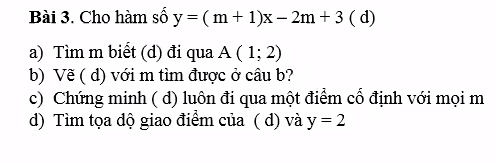
Đổi : 20 cm = 0,2 m
Cảm ứng từ tại tâm O :
\(B_o=2\pi.10^{-7}\dfrac{I}{r}=2\pi.10^{-7}\dfrac{3+4}{0,2}=7.10^{-6}\left(T\right)\)