Cho tam giác ABC. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm K sao cho MK = MA. a) Chứng minh rằng: tam giác AMB = tam giác KMC b) Trên cạnh AB, CK lần lượt lấy điểm E, F sao cho BE = CF. Chứng minh rằng: Ba điểm E, M, F thẳng hàng.( giúp mình với T^T)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét \(\Delta AMB\) và \(\Delta KMC\) có :
AM = MK ( gt )
\(\widehat{M_1}=\widehat{M_2}\) 9 đối đỉnh )
BM = MC ( gt )
=> \(\Delta AMB\) = \(\Delta KMC\)
b)
\(\Delta AMB\) =\(\Delta KMC\)
\(\Rightarrow\widehat{B_1}=\widehat{C_1}\)
Mà góc B1 l C1 so le trong
=> BA // KC

Lời giải:
a. Xét tam giác $AMC$ và $KMB$ có:
$MC=MB$ (do $M$ là trung điểm $BC$)
$AM=KM$ (gt)
$\widehat{AMC}=\widehat{KMB}$ (đối đỉnh)
$\Rightarrow \triangle AMC=\triangle KMB$ (c.g.c)
và $\widehat{ACM}=\widehat{KBM}$
Mà 2 góc này ở vị trí so le trong nên $AC\parallel BK$
b.
Xét tam giác $ABM$ và $KCM$ có:
$BM=CM$
$AM=KM$
$\widehat{AMB}=\widehat{KMC}$ (đối đỉnh)
$\Rightarrow \triangle ABM=\triangle KCM$ (c.g.c)
$\Rightarrow \widehat{ABM}=\widehat{KCM}$
Mà 2 góc này ở vị trí so le trong nên $AB\parallel CK$

a
vì AM là tia phân giác của góc A=>góc BAM=CAM
xét tam giác AMB và tam giác AMC có:
góc BAM=CAM,AM chung,AB=AC=>tam giác AMB = tam giác AMC
b
vì tam giác AMB = tam giác AMC=>MB=MC=>M là trung điểm BC
vì tam giác AMB = tam giác AMC=>góc BAM=CAM mà góc BAM+CAM=180=>BAM=CAM=180 độ/2=90 độ=>AM vuông góc với BC
c
xét tam giác ABM và KCM có
MB=MC,MA=MK,góc BMA=CMK(vì đối đỉnh)=>tam giác ABM = KCM=>AB=CK
vì tam giác ABM = KCM=>góc ABM=KMB mà 2 góc trên ở vị trí so le trog=>AB//CK

a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔMAB=ΔMDC
b: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: BA=DC; AC=DB
Xét ΔBAC và ΔCDB có
BA=CD
AC=DB
BC chung
Do đó: ΔBAC=ΔCDB
c: Xét tứ giác AEDF có
AE//DF
AE=DF
Do đó: AEDF là hình bình hành
Suy ra: AD và FE cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của AD
nên M là trung điểm của FE
hay F,M,E thẳng hàng

a: Xét tứ giác ABEC có
M là trung điểm của BC
M là trung điểm của AE
Do đó: ABEC là hình bình hành
Suy ra: AB//EC

a: Xét ΔMAC và ΔMDB có
MA=MD
\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔMAC=ΔMDB
b: Xét ΔMEB và ΔMFC có
ME=MF
\(\widehat{BME}=\widehat{CMF}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMEB=ΔMFC
=>\(\widehat{MEB}=\widehat{MFC}\)
=>\(\widehat{MFC}=90^0\)
=>CF\(\perp\)AD
c: Xét tứ giác BFCE có
M là trung điểm chung của BC và FE
=>BFCE là hình bình hành
=>BF//CE và BF=CE
Ta có: BF//CE
B\(\in\)FG
Do đó: BG//CE
Ta có: BF=CE
BF=BG
Do đó: BG=CE
Xét tứ giác BGEC có
BG//EC
BG=EC
Do đó: BGEC là hình bình hành
=>BE cắt GC tại trung điểm của mỗi đường
mà H là trung điểm của BE
nên H là trung điểm của GC
=>G,H,C thẳng hàng

b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: CD//AB

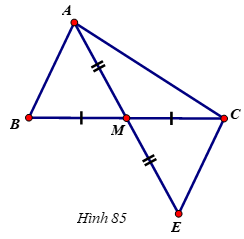
a: Xét ΔAMB và ΔEMC có
MA=ME
\(\widehat{AMB}=\widehat{EMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔAMB=ΔEMC
b: Ta có: ΔAMB=ΔEMC
=>AB=CE
Ta có: ΔAMB=ΔEMC
=>\(\widehat{MAB}=\widehat{MEC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//EC
c: Xét ΔHAM và ΔKEM có
HA=KE
\(\widehat{HAM}=\widehat{KEM}\)
AM=EM
Do đó: ΔHAM=ΔKEM
=>\(\widehat{AMH}=\widehat{EMK}\)
mà \(\widehat{AMH}+\widehat{HME}=180^0\)(hai góc kề bù)
nên \(\widehat{EMK}+\widehat{HME}=180^0\)
=>H,M,E thẳng hàng
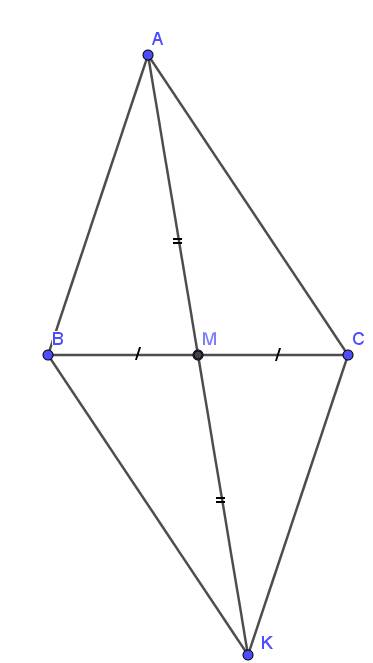
a: Xét ΔAMB và ΔKMC có
MA=MK
\(\widehat{AMB}=\widehat{KMC}\)
MB=MC
Do đó: ΔAMB=ΔKMC
b: Xét tứ giác BECF có
BE//CF
BE=CF
Do đó: BECF là hình bình hành
Suy ra: BC và EF cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của FE
hay F,M,E thẳng hàng