cho hàm số \(y{\rm{ }} = {\rm{ }}f\left( x \right){\rm{ }} = {\rm{ }}3{x^2} + {\rm{ }}1\) Tính f(-1) có kết quả bằng :
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Với a = 0, b = 1, hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{2x}&{{\rm{ }}x < 2}\\4&{{\rm{ }}x = 2}\\{ - 3x + 1}&{{\rm{ }}\,x > 2}\end{array}} \right.\)
Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( { - 3x + 1} \right) = - 3.2 + 1 = - 5\\\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {2x} \right) = 2.2 = 4\\ \Rightarrow \mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right)\end{array}\)
Do đó không tồn tại giới hạn \(\mathop {\lim }\limits_{x \to 2} f\left( x \right)\)
Vậy hàm số không liên tục tại x = 2.
b) Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( { - 3x + b} \right) = - 3.2 + b = - 6 + b\\\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {2x + a} \right) = 2.2 + a = 4 + a\\f\left( 2 \right) = 4\end{array}\)
Để hàm số liên tục tại x = 2 thì \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = f\left( 2 \right)\)
\( \Leftrightarrow - 6 + b = 4 + a = 4 \Leftrightarrow \left\{ \begin{array}{l}4 + a = 4\\ - 6 + b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = 10\end{array} \right.\)
Vậy với a = 0 và b = 10 thì hàm số liên tục tại x = 2.
c) Tập xác định của hàm số là: ℝ.
Với x < 2 thì \(f\left( x \right) = 2x + a\) là hàm đa thức nên liên tục.
Với x > 2 thì \(f\left( x \right) = -3x + b\) là hàm đa thức nên liên tục.
Do đó để hàm số liên tục trên ℝ thì hàm số \(f\left( x \right)\) liên tục tại x = 2.
Vậy với a = 0 và b = 10 thỏa mãn điều kiện.

a) \(y' = 2.3{{\rm{x}}^2} - \frac{1}{2}.2{\rm{x}} + 4.1 - 0 = 6{{\rm{x}}^2} - x + 4\).
b) \(y' = \frac{{{{\left( { - 2{\rm{x}} + 3} \right)}^\prime }.\left( {{\rm{x}} - 4} \right) - \left( { - 2{\rm{x}} + 3} \right).{{\left( {{\rm{x}} - 4} \right)}^\prime }}}{{{{\left( {{\rm{x}} - 4} \right)}^2}}}\)
\( = \frac{{ - 2\left( {{\rm{x}} - 4} \right) - \left( { - 2{\rm{x}} + 3} \right).1}}{{{{\left( {{\rm{x}} - 4} \right)}^2}}}\)
\( = \frac{{ - 2{\rm{x}} + 8 + 2{\rm{x}} - 3}}{{{{\left( {{\rm{x}} - 4} \right)}^2}}} = \frac{5}{{{{\left( {{\rm{x}} - 4} \right)}^2}}}\)
c) \(y' = \frac{{{{\left( {{x^2} - 2{\rm{x}} + 3} \right)}^\prime }\left( {{\rm{x}} - 1} \right) - \left( {{x^2} - 2{\rm{x}} + 3} \right){{\left( {{\rm{x}} - 1} \right)}^\prime }}}{{{{\left( {{\rm{x}} - 1} \right)}^2}}}\)
\( = \frac{{\left( {2{\rm{x}} - 2} \right)\left( {{\rm{x}} - 1} \right) - \left( {{x^2} - 2{\rm{x}} + 3} \right).1}}{{{{\left( {{\rm{x}} - 1} \right)}^2}}}\) \( = \frac{{2{{\rm{x}}^2} - 2{\rm{x}} - 2{\rm{x}} + 2 - {x^2} + 2{\rm{x}} - 3}}{{{{\left( {{\rm{x}} - 1} \right)}^2}}}\)
\( = \frac{{{x^2} - 2{\rm{x}} - 1}}{{{{\left( {{\rm{x}} - 1} \right)}^2}}}\)
d) \(y' = {\left( {\sqrt 5 .\sqrt x } \right)^\prime } = \sqrt 5 .\frac{1}{{2\sqrt x }} = \frac{{\sqrt 5 }}{{2\sqrt x }} = \frac{5}{{2\sqrt {5x} }}\).

\(a)\left( { - \frac{{3{\rm{x}}}}{{5{\rm{x}}{y^2}}}} \right):\left( { - \frac{{5{y^2}}}{{12{\rm{x}}y}}} \right) = \frac{{ - 3{\rm{x}}}}{{5{\rm{x}}{y^2}}}.\frac{{ - 12{\rm{x}}y}}{{5{y^2}}} = \frac{{36{{\rm{x}}^2}y}}{{25{\rm{x}}{y^4}}}\)
b) \(\frac{4{{\text{x}}^{2}}-1}{8{{\text{x}}^{3}}-1}:\frac{4{{\text{x}}^{2}}+4\text{x}+1}{4{{\text{x}}^{2}}+2\text{x}+1}=\frac{4{{\text{x}}^{2}}-1}{8{{\text{x}}^{3}}-1}.\frac{4{{\text{x}}^{2}}+2\text{x}+1}{4{{\text{x}}^{2}}+4\text{x}+1}\)
\(=\frac{\left( 2\text{x}-1 \right)\left( 2\text{x}+1 \right)\left( 4{{\text{x}}^{2}}+2\text{x}+1 \right)}{\left( 2\text{x}-1 \right)\left( 4{{\text{x}}^{2}}+2\text{x}+1 \right){{\left( 2\text{x}+1 \right)}^{2}}}=\frac{1}{2\text{x}+1}\).

a, \(y=3x^4-7x^3+3x^2+1\)
\(y'=12x^3-21x^2+6x\)
b, \(y=\left(x^2-x\right)^3\)
\(y'=3\left(x^2-x\right)^2\left(2x-1\right)\)
c, \(y=\dfrac{4x-1}{2x+1}\)
\(y'=\dfrac{4+2}{\left(2x+1\right)^2}\)
\(y'=\dfrac{6}{\left(2x+1\right)^2}\)
a: y=3x^4-7x^3+3x^2+1
=>y'=3*4x^3-7*3x^2+3*2x
=12x^3-21x^2+6x
b: \(y'=\left[\left(x^2-x\right)^3\right]'\)
\(=3\left(2x-1\right)\left(x^2-x\right)^2\)
c: \(y'=\dfrac{\left(4x-1\right)'\left(2x+1\right)-\left(4x-1\right)\left(2x+1\right)'}{\left(2x+1\right)^2}\)
\(=\dfrac{4\left(2x+1\right)-2\left(4x-1\right)}{\left(2x+1\right)^2}=\dfrac{6}{\left(2x+1\right)^2}\)

a) Tìm thương và dư (nếu có) trong các phép chia \(\left( {3{{\rm{x}}^4}y - 9{{\rm{x}}^3}{y^2} - 21{{\rm{x}}^2}{y^2}} \right):\left( {3{{\rm{x}}^2}y} \right)\)
• Sử dụng lệnh Division(<đa thức bị chia>, <đa thức chia>) để tìm thương và dư của phép chia hai đa thức.
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
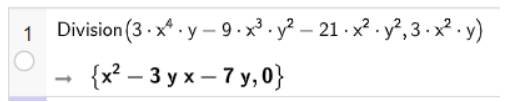
Vậy phép chia hai đa thức \(\left( {3{{\rm{x}}^4}y - 9{{\rm{x}}^3}{y^2} - 21{{\rm{x}}^2}{y^2}} \right)\) cho \(3{{\rm{x}}^2}y\), ta được thương là \({x^2} - 3{\rm{x}}y - 7y\) và dư 0.
b) Tìm thương và dư (nếu có) trong các phép chia (2x3 + 5x2 – 2x + 12) : (2x2 – x + 1).
• Sử dụng lệnh Division(<đa thức bị chia>, <đa thức chia>) để tìm thương và dư của phép chia hai đa thức.
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.

Vậy phép chia hai đa thức (2x3 + 5x2 – 2x + 12) cho (2x2 – x + 1), ta được thương là x + 3 và dư 9.

a) Đây là kết luận đúng vì: \( - 6.2{y^2} = - 3y.4y\)
b) Đây là kết luận đúng vì: \(5{\rm{x}}\left( {x + 3} \right) = 5\left( {{x^2} + 3{\rm{x}}} \right) = 5{{\rm{x}}^2} + 15{\rm{x}}\)
c) Đây là kết luận đúng vì: \(3{\rm{x}}\left( {4{\rm{x}} + 1} \right)\left( {1 - 4{\rm{x}}} \right) = 3{\rm{x}}\left( {1 - 16{{\rm{x}}^2}} \right) = - 3{\rm{x}}\left( {16{{\rm{x}}^2} - 1} \right)\)

Ta có: \(MF = \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} ,d\left( {M,\Delta } \right) = \left| {y + 1} \right|\).
Xét \(MF = d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} = \left| {y + 1} \right| \Leftrightarrow {x^2} + {\left( {y - 1} \right)^2} = {\left( {y + 1} \right)^2} \Leftrightarrow {x^2} = 4y \Leftrightarrow y = \frac{1}{4}{x^2}\).
Vậy tập hợp điểm M để \(MF{\rm{ }} = \;d\left( {M,\Delta } \right)\) là parabol \(y = \frac{1}{4}{x^2}\)

a) Ta có:
\(\begin{array}{l}C = {\left( {3{\rm{x}} - 1} \right)^2} + {\left( {3{\rm{x}} + 1} \right)^2} - 2\left( {3{\rm{x}} - 1} \right)\left( {3{\rm{x}} + 1} \right)\\C = {\left( {3{\rm{x}} - 1} \right)^2} - 2\left( {3{\rm{x}} - 1} \right)\left( {3{\rm{x}} + 1} \right) + {\left( {3{\rm{x}} + 1} \right)^2}\\C = {\left( {3{\rm{x}} - 1 - 3{\rm{x}} - 1} \right)^2}\\C = {\left( { - 2} \right)^2} = 4\end{array}\)
Vậy giá trị của biểu thức C = 4 không phụ thuộc vào biến x
b) Ta có:
\(\begin{array}{l}D = {\left( {x + 2} \right)^3} - {\left( {x - 2} \right)^3} - 12\left( {{x^2} + 1} \right) \\D = \left( {x + 2 - x + 2} \right)\left[ {{{\left( {x + 2} \right)}^2} + \left( {x + 2} \right)\left( {x - 2} \right) + {{\left( {x - 2} \right)}^2}} \right] - 12{{\rm{x}}^2} - 12\\D = 4.\left( {{x^2} + 4{\rm{x}} + 4 + {x^2} - 4 + {x^2} - 4{\rm{x}} + 4} \right) - 12{{\rm{x}}^2} - 12\\D = 4.\left( {3{{\rm{x}}^2} + 4} \right) - 12{{\rm{x}}^2} - 12\\D = 12{{\rm{x}}^2} + 16 - 12{{\rm{x}}^2} - 12 = 4\end{array}\)
Vậy giá trị của biểu thức D = 4 không phụ thuộc vào biến x
c) Ta có:
\(\begin{array}{l}E = \left( {x + 3} \right)\left( {{x^2} - 3{\rm{x}} + 9} \right) - \left( {x - 2} \right)\left( {{x^2} + 2{\rm{x}} + 4} \right)\\E = \left( {{x^3} + {3^3}} \right) - \left( {{x^3} - {2^2}} \right)\\E = {x^3} + 27 - {x^3} + 8 = 35\end{array}\)
Vậy giá trị của biểu thức E = 35 không phụ thuộc vào biến x
d) Ta có:
\(\begin{array}{l}G = \left( {2{\rm{x}} - 1} \right)\left( {4{{\rm{x}}^2} + 2{\rm{x}} + 1} \right) - 8\left( {x + 2} \right)\left( {{x^2} - 2{\rm{x}} + 4} \right)\\G = \left[ {{{\left( {2{\rm{x}}} \right)}^3} - {1^3}} \right] - 8\left( {{x^3} + {2^3}} \right)\\G = 8{{\rm{x}}^3} - 1 - 8{{\rm{x}}^3} - 64 = - 65\end{array}\)
Vậy giá trị của biểu thức G = -65 không phụ thuộc vào biến x.
f(-1)=4
\(=3.\left(-1\right)^2+1=3.1+1=3+1=4\)