Đa thức x3−3x+a chia cho đa thức x – 1 có số dư là 1 thì a bằng : a. 3 b. 1 c. 4 d. 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 11 2019
a) A = ( x 2 – 6x)B.
b) A = (-x – 8)B + 2
c) A = (x + 3)B + 6.
4 tháng 10 2023
2) Ta có đẳng thức sau: \(\left(a+b\right)\left(b+c\right)\left(c+a\right)=\left(a+b+c\right)\left(ab+bc+ca\right)-abc\)
Chứng minh thì bạn chỉ cần bung 2 vế ra là được.
\(\Rightarrow P=\left(a+b+c\right)\left(ab+bc+ca\right)-2abc\)
Do \(a+b+c⋮4\) nên ta chỉ cần chứng minh \(abc⋮2\) là xong. Thật vậy, nếu cả 3 số a, b,c đều không chia hết cho 2 thì \(a+b+c\) lẻ, vô lí vì \(a+b+c⋮4\). Do đó 1 trong 3 số a, b, c phải chia hết cho 2, suy ra \(abc⋮2\).
Do đó \(P⋮4\)
AH
Akai Haruma
Giáo viên
18 tháng 11 2021
Lời giải:
Ta có:
$2x^4-3x^3-3x-2=2x^2(x^2-1)-3x(x^2-1)+2x^2-6x-2$
$=(2x^2-3x)(x^2-1)+2(x^2-1)-6x$
$=(2x^2-3x+2)(x^2-1)-6x$
Vậy $2x^4-3x^3-3x-2$ chia $x^2-1$ dư $-6x$
Không có đáp án nào đúng
19 tháng 9 2023
a) Ta có:
B = (A + B) – A
= (x3 + 3x + 1) – (x4 + x3 – 2x – 2)
= x3 + 3x + 1 – x4 - x3 + 2x + 2
= – x4 + (x3 – x3) + (3x + 2x) + (1 + 2)
= – x4 + 5x + 3.
b) C = A - (A – C)
= x4 + x3 – 2x – 2 – x5
= – x5 + x4 + x3 – 2x – 2.
c) D = (2x2 – 3) . A
= (2x2 – 3) . (x4 + x3 – 2x – 2)
= 2x2 . (x4 + x3 – 2x – 2) + (-3) .(x4 + x3 – 2x – 2)
= 2x2 . x4 + 2x2 . x3 + 2x2 . (-2x) + 2x2 . (-2) + (-3). x4 + (-3) . x3 + (-3). (-2x) + (-3). (-2)
= 2x6 + 2x5 – 4x3 – 4x2 – 3x4 – 3x3 + 6x + 6
= 2x6 + 2x5 – 3x4 + (-4x3 – 3x3) – 4x2+ 6x + 6
= 2x6 + 2x5 – 3x4 – 7x3 – 4x2+ 6x + 6.
d) P = A : (x+1) = (x4 + x3 – 2x – 2) : (x + 1)
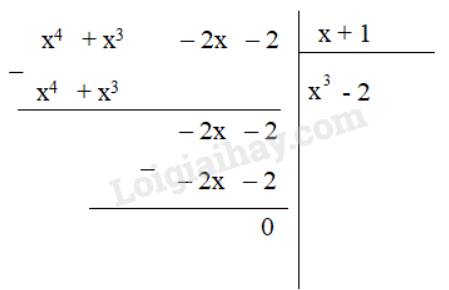
Vậy P = x3 - 2
e) Q = A : (x2 + 1)
Nếu A chia cho đa thức x2 + 1 không dư thì có một đa thức Q thỏa mãn
Ta thực hiện phép chia (x4 + x3 – 2x – 2) : (x2 + 1)
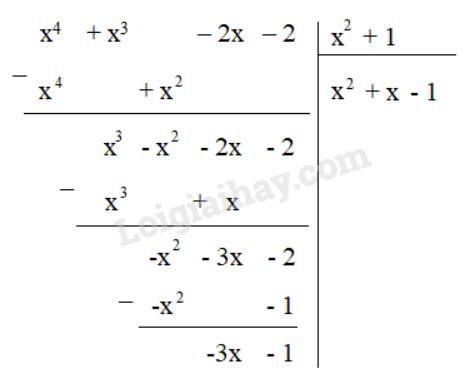
Do phép chia có dư nên không tồn tại đa thức Q thỏa mãn
24 tháng 2 2021
Vì \(f\left(x\right)⋮x-2;f\left(x\right):x^2-1\) dư 1\(\Rightarrow\left\{{}\begin{matrix}f\left(x\right)=g\left(x\right)\cdot\left(x-2\right)\\f\left(x\right)=q\left(x\right)\left(x^2-1\right)+x=q\left(x\right)\left(x-1\right)\left(x+1\right)+x\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}f\left(2\right)=0\\f\left(1\right)=1\\f\left(-1\right)=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}32+4a+2b+c=0\\2+a+b+c=1\\2+a-b+c=-1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}4a+2b+c=-32\left(1\right)\\a+b+c=-1\left(2\right)\\a-b+c=-3\left(3\right)\end{matrix}\right.\)
Trừ từng vế của (2) cho (3) ta được:
\(\Rightarrow2b=2\Rightarrow b=1\)
Thay b=1 vào lần lượt (1) ,(2),(3) ta được:
\(\Rightarrow\left\{{}\begin{matrix}4a+2+c=-32\\a+1+c=-1\\a-1+c=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4a+c=-34\\a+c=-2\\a+c=-2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}4a+c=-34\left(4\right)\\a+c=-2\left(5\right)\end{matrix}\right.\)
Trừ từng vế của (4) cho (5) ta được:
\(\Rightarrow3a=-32\Rightarrow a=-\dfrac{32}{3}\Rightarrow c=-2+\dfrac{32}{3}=\dfrac{26}{3}\) Vậy...
Áp dụng định lí Bezout ta có dư của phép chia x3 - 3x + a cho x - 1 là R = f(1)
=> f(1) = 13 - 3 . 1 + a
= 1 - 3 + a
= a - 2
Mà R = 1
=> f(1) = 1
=> a - 2 = 1
=> a = 1 + 2
a = 3
=>A
Chọn D