Cho tam giác ABC có độ dài các cạnh là AB = 12 cm , AC = 9 cm , BC = 15 cm . Kẻ AH vuông góc BC tại H .
a) CMR : Tam giác ABC vuông tại A . Tính số đo các góc nhọn của tam giác .
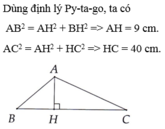
b) Tính độ dài cạnh AH , HB .
c) Trên tia đối AC lấy D sao cho góc ABD = 30 độ . Hãy tính độ dài các cạnh của tam giác BAD .
Trên cạnh AC lấy I sao cho IH = IA . Từ I kẻ đường thẳng song song AH cắt BC tại K . CMR : \(BK^2=KC^2+AB^2\)