Hãy vẽ hình tam giác ABC có ba góc nhọn rồi vẽ đường cao AD,BE,CG của hình tam giác đó . Em có nhận xét gì về các đường cao AD,BE,CG của hình tam giác này
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Xét (O) có
ΔABM nội tiếp
AM là đường kính
Do đó: ΔABM vuông tại B
=>BM\(\perp\)AB
mà CH\(\perp\)AB
nên CH//BM
Xét (O) có
ΔACM nội tiếp
AM là đường kính
Do đó: ΔACM vuông tại C
=>AC\(\perp\)CM
mà BH\(\perp\)AC
nên BH//CM
Xét tứ giác BHCM có
BH//CM
BM//CH
Do đó: BHCM là hình bình hành
b:
Xét ΔABC có
BE,CF là các đường cao
BE cắt CF tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại D
Xét (O) có
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
\(\widehat{AMC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{ABC}=\widehat{AMC}\)
Ta có: \(\widehat{ABC}+\widehat{BAN}=90^0\)(ΔADB vuông tại D)
\(\widehat{AMC}+\widehat{MAC}=90^0\)(ΔACM vuông tại C)
mà \(\widehat{ABC}=\widehat{AMC}\)
nên \(\widehat{BAN}=\widehat{MAC}\)
Xét (O) có
ΔANM nội tiếp
AM là đường kính
Do đó: ΔANM vuông tại N
=>AN\(\perp\)NM
mà AN\(\perp\)BC
nên BC//NM
Ta có: \(\widehat{CHD}=\widehat{ABC}\)(=90 độ-góc FCB)
\(\widehat{ABC}=\widehat{ANC}\)
Do đó: \(\widehat{CHD}=\widehat{ANC}\)
=>ΔCHN cân tại C
=>CH=CN
mà CH=BM
nên BM=CN
Xét tứ giác BCMN có BC//MN
nên BCMN là hình thang
Hình thang BCMN có BM=CN
nên BCMN là hình thang cân

a: góc AEB=góc ADB=90 độ
=>AEDB nội tiếp
b,c: M ở đâu vậy bạn?

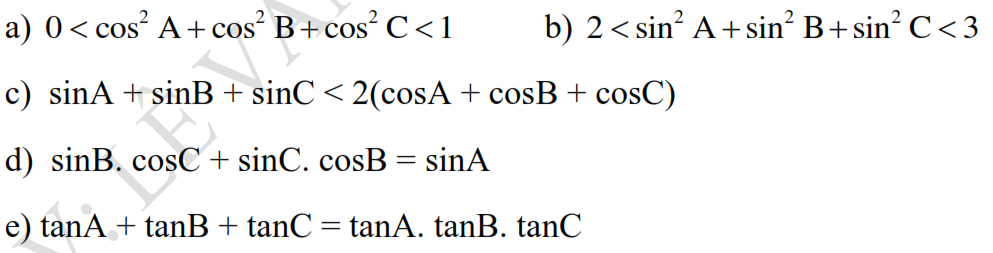
Mình đag cần nhanh giúp mnhf với
Ba đường này cắt nhau tại một điểm gọi là trực tâm của tam giác