Tìm x thuộc Z, biết:
x-6 chia hết cho x+3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


C1
Câu trả lời hay nhất: Bài này có nhiều cách giải khác nhau:
C1: Nhận vào: 5x^2-16x+3=0, giải phương trình bậc 2 => x=3, x=1/5
C2: Đặt nhân tử chung:
5x(x-3)-(x-3)=0 <=> (x-3)(5x-1)=0 <=> x-3=0 hoặc 5x-1=0
<=> x=3, x=1/5
C2

x+10 chia hết cho 5 mà 10 chia hết cho 5,suy ra x chia hết cho 5
x-18 chia hết cho 6 mà 18 chia hết cho 6,suy ra x chia hết cho 6
x+21 chia hết cho 7 mà 21 chia hết cho 7 ,suy ra x chia hết cho 7
Vậy x thuộc BC(5,6,7)
5=5
6=2.3
7=7
BCNN(5,6,7)=2.3.5.7=210
biết BC(5,6,7)=B(210)={0;210;420;630;...}
mà x<700 nên x thuộc {0;210;420;630;...}
Vậy x thuộc {0;210;420;630;...}
x là số tự nhiên phải k
\(x+10⋮5\Rightarrow x+10\in B\left(5\right)=\left\{0;5;10;15;...\right\}\)
\(\Rightarrow x\in\left\{0;5;...\right\}\)
\(x-18⋮6\Rightarrow x-18\in B\left(6\right)=\left\{0;6;12;18;...\right\}\)
\(\Rightarrow x\in\left\{18;24;30;36;...\right\}\)
\(x+21⋮7\Rightarrow x+21\in B\left(7\right)=\left\{0;7;14;21;28;35...\right\}\)
\(\Rightarrow x\in\left\{0;7;14;...\right\}\)
Mà x < 700 \(\Rightarrow x\in\left\{0;7;14;...;693\right\}\)

6 \(n^5+5n=n^5-n+6n=n\left(n^4-1\right)+6n=n\left(n^2-1\right)\left(n^2+1\right)+6n\)
\(=n\left(n-1\right)\left(n+1\right)\left(n^2+1\right)+6n\)
vì n,n-1 là 2 số nguyên lien tiếp \(\Rightarrow n\left(n-1\right)⋮2\Rightarrow n\left(n-1\right)\left(n+1\right)\left(n^2+1\right)⋮2\)
n,n-1,n+1 là 3 sô nguyên liên tiếp \(\Rightarrow n\left(n-1\right)\left(n+1\right)⋮3\Rightarrow n\left(n-1\right)\left(n+1\right)\left(n^2+1\right)⋮3\)
\(\Rightarrow n\left(n-1\right)\left(n+1\right)\left(n^2+1\right)⋮2\cdot3=6\)
\(6⋮6\Rightarrow6n⋮6\Rightarrow n\left(n-1\right)\left(n+1\right)\left(n^2+1\right)-6n⋮6\Rightarrow n^5+5n⋮6\)(đpcm)
7 \(n\left(2n+7\right)\left(7n+1\right)=n\left(2n+7\right)\left(7n+7-6\right)=7n\left(n+1\right)\left(2n+7\right)-6n\left(2n+7\right)\)
\(=7n\left(n+1\right)\left(2n+4+3\right)-6n\left(2n+7\right)\)
\(=7n\left(n+1\right)\left(2n+4\right)+21n\left(n+1\right)-6n\left(2n+7\right)\)
\(=14n\left(n+1\right)\left(n+2\right)+21n\left(n+1\right)-6n\left(2n+7\right)\)
n,n+1,n+2 là 3 sô nguyên liên tiếp dựa vào bài 6 \(\Rightarrow n\left(n+1\right)\left(n+2\right)⋮6\Rightarrow14n\left(n+1\right)\left(n+2\right)⋮6\)
\(21⋮3;n\left(n+1\right)⋮2\Rightarrow21n\left(n+1\right)⋮3\cdot2=6\)
\(6⋮6\Rightarrow6n\left(2n+7\right)⋮6\)
\(\Rightarrow14n\left(n+1\right)\left(n+2\right)+21n\left(n+1\right)-6n\left(2n+7\right)⋮6\)
\(\Rightarrow n\left(2n+7\right)\left(7n+1\right)⋮6\)(đpcm)
......................?
mik ko biết
mong bn thông cảm
nha ................


xy + 2x - 3y = 9
\(\Leftrightarrow\) 2x + xy - 3y - 6 = 3
\(\Leftrightarrow\) x(2 + y) - 3(y + 2) = 3
\(\Leftrightarrow\) (2 + y)(x - 3) = 3
Vì x, y \(\in\) Z nên (2 + y)(x - 3) \(\in\) Z. Ta có bảng sau:
| x - 3 | 3 | 1 | -1 | -3 |
| 2 + y | 1 | 3 | -3 | -1 |
| x | 6(TM) | 4(TM) | 2(TM) | 0(TM) |
| y | -1(TM) | 1(TM) | -5(TM) | -3(TM) |
Vậy phương trình có nghiệm (x; y) = {(6; 1); (4; 1); (2; -5); (0; -3)}
Chúc bn học tốt!

a) x Î Ư(6) = {-6; -3; -2; -l; l; 2; 3; 6}.
b) x + l Î Ư (8) = {- 8; -4; -2; -1; 1; 2; 4; 8}. Từ đó tìm được
x Î{-9; -5; -3; -2; 0; 1; 3; 7}.
c) x - 2 Î Ư(10) = {-10; -5; - 2; -1; 1; 2; 5; 10). Từ đó tìm được
x Î {-8; -3; 0; l; 3; 5; 7; 12}.
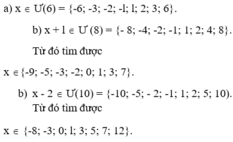
\(\Leftrightarrow x+3\in\left\{1;-1;3;-3;9;-9\right\}\)
hay \(x\in\left\{-2;-4;0;-6;6;-12\right\}\)
\(\dfrac{x-6}{x+3}=\dfrac{x+3-6}{x+3}=\dfrac{x+3}{x+3}-\dfrac{6}{x+3}=1-\dfrac{6}{x+3}\)
\(\dfrac{x-6}{x+3}⋮x+3\Rightarrow\dfrac{6}{x+3}⋮x+3\\ \Rightarrow x+3\inƯ_{\left(6\right)}=\left\{-6;-3;-2;-1;1;2;3;6\right\}\)
\(\Rightarrow x\in\left\{-9;-6;-5;-4;-2;-1;0;3\right\}\)