Từ 1 điểm A nắm ngoài đường tròn (o) kẻ 2 tiếp tuyến AB AC đền đg tròn (O) (B và C là các tiếp điểm) và một cát tuyến ADE không đi qua tâm O ( D nằm giữa A và E), gọi I là trung điểm của DE
Bạn chỉ mình cách vẽ với nha mình bí ở cái cát tuyến rồi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Cho đường tròn tâm (O). Từ điểm S ở ngoài đường tròn (O) kẻ các tiếp tuyến SA và SB với (O) (A, B là các tiếp điểm). Kẻ cát tuyến SCD không đi qua tâm O (C nằm giữa S và D). Gọi I là trung điểm của CD.a/ Chứng minh các điểm S, A, I, O, B cùng nằm trên một đường tròn.b/ Chứng minh IS là đường phân giác của góc AIB.c/ Gọi M là giao điểm của hai đường thẳng SO và AB; N là giao điểm của hai đường thẳng SD và AB. Chứng minh MC.ND = NC.MD
14 tháng 7 2023
a: ΔOED cân tại O có OF là trung tuyến
nên OF vuông góc ED
góc OFA=góc OBA=góc OCA=90 độ
=>O,F,B,A,C cùng thuộc 1 đường tròn
b: góc DHC=góc CBA
góc CBA=góc DFC
=>góc DHC=góc DFC
2 tháng 1
a: Xét tứ giác ABOC có \(\widehat{ABO}+\widehat{ACO}=90^0+90^0=180^0\)
nên ABOC là tứ giác nội tiếp
=>A,B,O,C cùng thuộc một đường tròn
b: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AO là đường trung trực của BC
=>AO\(\perp\)BC tại trung điểm H của BC
Gọi K là giao điểm của OS và ED
Xét (O) có
SE,SD là các tiếp tuyến
Do đó: SE=SD
=>S nằm trên đường trung trực của ED(3)
Ta có: OE=OD
=>O nằm trên đường trung trực của ED(4)
Từ (3) và (4) suy ra SO là đường trung trực của ED
=>SO\(\perp\)ED tại trung điểm K của ED
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2=R^2\left(5\right)\)
Xét ΔODS vuông tại D có DK là đường cao
nên \(OK\cdot OS=OD^2=R^2\left(6\right)\)
Từ (5) và (6) suy ra \(OH\cdot OA=OK\cdot OS\)
=>\(\dfrac{OH}{OK}=\dfrac{OS}{OA}\)
Xét ΔOHS và ΔOKA có
\(\dfrac{OH}{OK}=\dfrac{OS}{OA}\)
góc HOS chung
Do đó: ΔOHS đồng dạng với ΔOKA
=>\(\widehat{OHS}=\widehat{OKA}\)
=>\(\widehat{OHS}=90^0\)
=>HO\(\perp\)SH tại H
mà HO\(\perp\)BH tại H
và SH,BH có điểm chung là H
nên S,H,B thẳng hàng
mà H,B,C thẳng hàng
nên S,B,H,C thẳng hàng
=>S,B,C thẳng hàng
6 tháng 3 2021
a) Xét tứ giác ABOC có
\(\widehat{ABO}\) và \(\widehat{ACO}\) là hai góc đối
\(\widehat{ABO}+\widehat{ACO}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ABOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABO vuông tại B có BH là đường cao ứng với cạnh huyền OA, ta được:
\(AH\cdot AO=AB^2\)(1)
Xét (O) có
\(\widehat{ABD}\) là góc tạo bởi tiếp tuyến BA và dây cung BD
\(\widehat{BED}\) là góc nội tiếp chắn \(\stackrel\frown{BD}\)
Do đó: \(\widehat{ABD}=\widehat{BED}\)(Hệ quả góc tạo bởi tiếp tuyến và dây cung)
hay \(\widehat{ABD}=\widehat{AEB}\)
Xét ΔABD và ΔAEB có
\(\widehat{ABD}=\widehat{AEB}\)
\(\widehat{BAD}\) chung
Do đó: ΔABD∼ΔAEB(g-g)
Suy ra: \(\dfrac{AB}{AE}=\dfrac{AD}{AB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB^2=AE\cdot AD\)(2)
Từ (1) và (2) suy ra \(AH\cdot AO=AD\cdot AE\)(đpcm)
26 tháng 6 2023
a: ΔODE cân tại O
mà OI là trung tuyến
nên OI vuông góc DE
góc OIA=góc OBA=góc OCA=90 độ
=>O,I,B,A,C cùng thuộc 1 đường tròn
b: góc BIA=góc BOA
góc CIA=góc COA
mà góc BOA=góc COA
nên góc BIA=góc CIA
=>IA là phân giác của góc BIC
11 tháng 10 2023
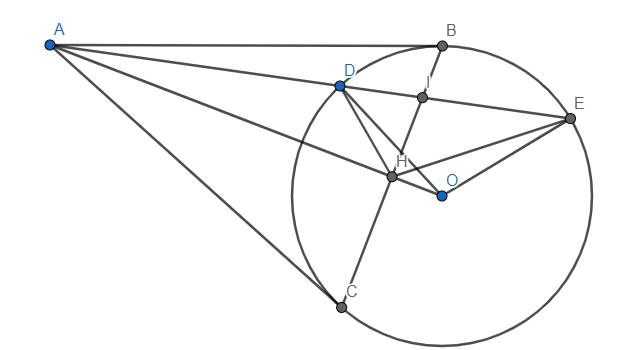
a) Do AB, AC tiếp xúc (O) tại B, C nên \(\widehat{OBA}=90^o\) và \(OA\perp BC\) tại H.
Xét tam giác OAB vuông tại B có đường cao BH, ta có \(OB^2=OA.OH\)
Mà \(OB=OD\left(=R_{\left(O\right)}\right)\) nên \(OD^2=OA.OH\). Từ đó suy ra \(\dfrac{OD}{OA}=\dfrac{OH}{OD}\). Từ đó dễ dàng suy ra 2 tam giác OHD và ODA đồng dạng.
b) Tam giác OAB vuông tại B có đường cao BH nên \(AB^2=AH.AO\)
Mặt khác, ta có \(\widehat{ABD}=\widehat{AEB}\) vì chúng lần lượt là góc tạo bởi tiếp tuyến, dây cung và góc nội tiếp cùng chắn cung BD.
\(\Rightarrow\Delta ABD~\Delta AEB\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AE}=\dfrac{AD}{AB}\Rightarrow AB^2=AD.AE\)
Từ đó suy ra \(AH.AO=AD.AE\) hay \(\dfrac{AH}{AD}=\dfrac{AE}{AO}\). Do đó \(\Delta AHE~\Delta ADO\left(c.g.c\right)\) \(\Rightarrow\widehat{AEH}=\widehat{AOD}\) hay tứ giác OHDE nội tiếp.
\(\Rightarrow\widehat{AHD}=\widehat{DEO}=\widehat{ODE}=\widehat{OHE}\)
\(\Rightarrow90^o-\widehat{AHD}=90^o-\widehat{OHE}\) \(\Rightarrow\widehat{DHI}=\widehat{EHI}\).
Ta suy ra được đpcm.
16 tháng 6 2023
a: góc OBA+góc OCA=180 độ
=>OBAC nội tiếp
b: Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>AH*AO=AB^2
Xét ΔABD và ΔAEB có
góc ABD=góc AEB
góc BAD chung
=>ΔABD đồng dạng với ΔAEB
=>AB^2=AD*AE=AH*AO
cát tuyến là đường thẳng cắt đường tròn tại 2 điểm
mà làm sao để em vẽ đc cát tuyến mà điểm thứ nhất cắt đg tròn nắm giữa điểm đầu và điểm cắt đg tròn thứ 2