các bạn giúp mình với
cho tam giác MNP nhọn(MN<MP).gọi I là trung điểm của NP.trên tia đối tia IM lấy điểm K sao cho I là trung điểm của MK
a) chứng minh rằng tam giác MIP=tam giác KIN
b) vẽ ND┴MP(D thuộc MP)
c) vẽ MH┴NP(H thuộc NP), trên tia đối của tia HM lấy điểm E sao cho HE=HM. chứng minh : PE=NK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 3 2022
Xét $\Delta MNH$ và $\Delta P$ ta có:
$\large \widehat{MHN}=\widehat{MPT}=90^o$
$\large \widehat{MNP}=\widehat{MTP}$(Hai góc cùng chắn cung $MP$)
Do đó $\large \Delta MNH \sim \Delta MTP$ $(g-g)$
Từ đó: $\frac{MN}{MT}=\frac{MH}{MP}\Leftrightarrow MN.MP=MH.MT$
Xét tứ giác $NQKP$ ta có:
$\large \widehat{NQP}=\widehat{PKN}=90^o$
Mà hai góc này cùng chắn cung $NP$
Do đó tứ giác $NQKP$ là tứ giác nội tiếp
Suy ra: $\large \widehat{PKQ}+\widehat{PNQ}=180^o$ (Hai góc nội tiếp đối nhau)
Đồng thời ta có $\large \widehat{PKQ}+\widehat{MKQ}=180^o\Rightarrow \widehat{MNP}=\widehat{MTP}=\widehat{MKQ}$
Gọi $A$ là giao điểm của $QK$ và $MT$
Xét tứ giác $TPKA$ ta có:
$\large \widehat{MTP}+\widehat{PKQ}=\widehat{PKQ}+\widehat{MKQ}=180^o$
Mà hai góc này ở vị trí đối nhau nên tứ giác $TPAK$ là tứ giác nội tiếp
$\large \Leftrightarrow \widehat{MPT}+\widehat{TAK}=180^o\Leftrightarrow \widehat{TAK}=180^o-\widehat{MPT}=90^o$
Do đó $MT$ vuông góc với $QK$
Hình:
29 tháng 3 2022
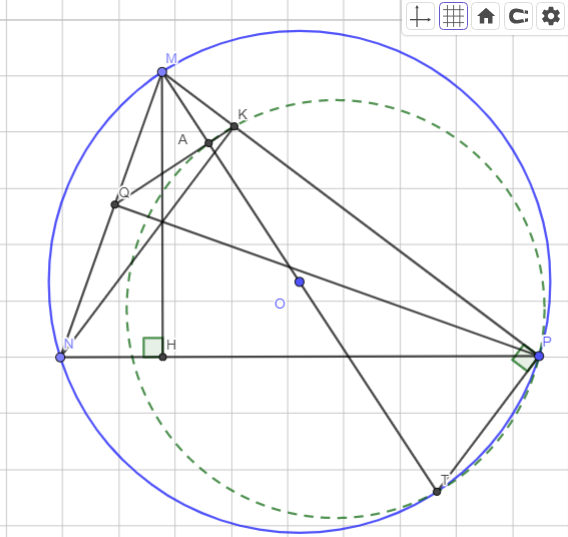
Dạ bài anh có nhầm lẫn gì kh ạ chứ khúc đầu e thấy hơi sai sai 😅😅
17 tháng 4 2022
a, Áp dụng Đ. L. py-ta-go vào tg ABC cân tại A, có:
BC2=AC2+AB2
=>152=AC2+92
225=AC2+81
=>AC=225-81
=144.
=>AC=12cm.
b, Xét tg ABM và tg NCM, có:
MB=MC(M là trung điển của BC)
góc AMB= góc CMN(đối đỉnh)
AM=NM(gt)
=>tg ABM= tg NCM(c. g. c)
=>góc ABM= góc NCM(2 góc tương ứng)
c, Ta có: góc BAC+ góc DAC=180o
=>góc DAC= 180o- góc BAC
=180o-90o
=90o
Xét tg ACB và tg ACD, có:
AB=AD(A là trung điểm của BC)
góc BAC = góc DAC(=90o)
AC chung
=>tg ABC= tg ADC(2 cạnh góc vuông)
=>BC=DC(2 cạnh tương ứng)
=>tg CBD cân tại C(đpcm)
18 tháng 3 2023
a: Xét ΔIMB vuông tại M và ΔIKC vuông tại K có
góc MIB=góc KIC
=>ΔIMB đồng dạng vơi ΔIKC
=>IM/IK=IB/IC
=>IM*IC=IB*IK
b: Xét ΔIMA vuông tạiM và ΔIEC vuông tại E có
góc MIA=góc EIC
=>ΔIMA đồng dạng với ΔIEC
=>IM/IE=IA/IC
=>IM*IC=IA*IE
c: Xét ΔAKI vuông tại K và ΔAEC vuông tại E có
góc KAI chung
=>ΔAKI đồng dạng với ΔAEC
=>AK/AE=AI/AC
=>AK*AC=AE*AI
d: Xet ΔAKB vuông tại K và ΔAMC vuông tại M có
góc KAB chung
=>ΔAKB đồng dạng với ΔAMC
=>AK/AM=AB/AC
=>AK*AC=AM*AB
27 tháng 7 2023
a: NP=căn 3^2+4^2=5cm
b: Xét ΔNMK vuông tại M và ΔNHK vuông tại H có
NK chung
góc MNK=góc HNK
=>ΔNMK=ΔNHK
c: Xét ΔKMI vuông tại M và ΔKHP vuông tại H có
KM=KH
góc MKI=góc HKP
=>ΔKMI=ΔKHP
=>KI=KP
=>KP>MI
17 tháng 3 2018
tự vẽ hình nha
a) xét tam giác MEN và tam giác MFP có:
\(\widehat{MFP}=\widehat{MEN}\left(=90'\right)\)
\(chung\widehat{NMP}\)
suy ra tam giác MEN đồng dạng với tam giác MFP (g-g)
do tam giác MEN đồng dạng với tam giác MFP
\(\Rightarrow\frac{ME}{MF}=\frac{MN}{MP}\)
lại có \(\widehat{NMP}\) chung
suy ra tam giác MFE đồng dạng với tam giác MPN
\(\Rightarrow\widehat{MEF}=\widehat{MNP}\)
HN
2 tháng 1 2022
cho tam giác MNP có 3 góc nhọn (MN<MP), A là trung điểm của cạnh NP. trên tia MA lấy D sao cho MA=AD.
a) chứng minh rằng tam giác mna= tam giác DPA.
b) chứng minh MN//PD.
c) chứng minh MP=ND.
a: Xét ΔMIP và ΔKIN có
IM=IK
\(\widehat{MIP}=\widehat{KIN}\)
IP=IN
Do đó: ΔMIP=ΔKIN
c: Xét ΔMEK có
H là trung điểm của ME
I là trung điểm của MK
Do đó: HI là đường trung bình
=>HI//EK và HI=EK/2
Xét ΔMPE có
PH là đường cao
PH là đường trung tuyến
Do đó: ΔMPE cân tại P
Suy ra: PM=PE(1)
Xét tứ giác MNKP có
I là trung điểm của MK
I là trung điểm của NP
Do đó: MNKP là hình bình hành
Suy ra: NK=MP(2)
Từ (1) và (2) suy ra NK=PE