Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Om nằm giữa tia Oy và On
nÔm = mÔy = 1800 - 1200 = 600
=>xOm = xÔm - nÔm = 1200 - 600 = 600
Vậy a = 600
Để Om nằm giữa Oy và On thì xOm < xOn
Mà xOm = 120o
Nên 180o < hoặc = xOn > 120o
+) Ta có: x O m ^ = 30 0 , y O n ^ = 2 x O m ^ = 2.30 0 = 60 0 Vì x O m ^ + m O y ^ = x O y ^ = 180 0 (hai góc kề bù) => m O y ^ = 180 0 − x O m ^ = 180 0 − 30 0 = 150 0 +) Xét trên nửa mặt phẳng có bờ chứa tia Oy, có : y O n ^ < y O m ^ (vì 0 ° < 60 ° < 150 ° ) => Tia On nằm giữa hai tia Oy và Om ⇒ m O n ^ + n O y ^ = m O y ^ = 150 0 ⇒ m O n ^ + 60 0 = 150 0 ⇒ m O n ^ = 150 0 − 60 0 ⇒ m O n ^ = 90 0 ⇒ O m ⊥ O n . |
Đáp án là D
Vì tia On là tia phân giác của ∠yOm nên ∠yOm = 2.∠yOn = 2. 70 0 = 140 0
Lại có xOy là góc bẹt nên ∠xOm và ∠yOm là hai góc kề bù
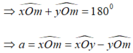
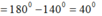
Vậy a = 40 0
\(A)\)
\(B)\)
Theo đề ra: Góc xOy là góc bẹt => Góc xOy = 180 độ
Góc xOm = 60 độ
=> Góc xOy > góc xOm => Tia Om nằm giữa hai tia Ox và Oy
Ta có: mOy = xOy - xOm
mOy = 180 độ - 60 độ
mOy = 120 độ
Ta có: mOn = yOn - mOy
mOn = 150 độ - 120 độ
mOn = 30 độ
\(C)\)
Ta có: xOn = xOm - mOn
xOn = 60 độ - 30 độ
xOn = 30 độ
=> Góc xOn = góc mOn
=> Tia On là tia phân giác của góc xOm
