cho tam giác ABC vuông tại A,kẻ đường cao AH.kẻ HD vuông góc với Ab tại D và kẻ HE vuông góc với Ac tại E.chứng minh tam giác ABC đồng dạng tam giác AEd
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 3 2016
Mình đã giải xong câu a, b, c. Nhờ các bạn và quý thầy cô giải giúp câu d. Chỉ cần tóm tắt lời giải thôi cũng được ạ.
HS
26 tháng 3 2016
d) SADE = 1/2.AD.AE ; SABC = 1/2.AB.AC => SADE / SABC = AD.AE/AB.AC =1/4 (1)
Do tg ADE đồng dạng tg ABC => SADE / SABC = (DE/BC)2 = (AH/BC)2 (2)
Từ (1) và (2) => AH/BC = 1/2 hay AH = !/2 BC. Vậy AH là đường trung tuyến tg ABC, mà AH là đường cao => tg ABC cân tại A
2 tháng 1 2023
a: Xét tứ giác ADHE có
góc ADH=góc AEH=góc DAE=90 độ
nên ADHE là hình chữ nhật
b: Vì ADHE là hình chữ nhật
nên AH=DE
c: Để ADHE là hình vuông thì AH là phân giác của góc DAE
mà AH vuông góc vơi BC
nên ΔABC cân tại A
=>AB=AC
AH
Akai Haruma
Giáo viên
30 tháng 3 2023
Lời giải:
a. Xét tam giác $AHB$ và $CAB$ có:
$\widehat{AHB}=\widehat{CAB}=90^0$
$\widehat{B}$ chung
$\Rightarrow \triangle AHB\sim \triangle CAB$ (g.g)
b. Từ tam giác đồng dạng phần a suy ra:
$\frac{HB}{AB}=\frac{AB}{CB}$
$\Rightarrow HB=\frac{AB^2}{BC}=\frac{AB^2}{\sqrt{AB^2+AC^2}}=\frac{15^2}{\sqrt{15^2+20^2}}=9$ (cm)
c. Xét tam giác $AHD$ và $ABH$ có:
$\widehat{A}$ chung
$\widehat{ADH}=\widehat{AHB}=90^0$
$\Righarrow \triangle AHD\sim \triangle ABH$ (g.g)
$\Rightarrow \frac{AH}{AB}=\frac{AD}{AH}$
$\Rightarrow AB.AD=AH^2(*)$
Tương tự ta cũng chỉ ra $\triangle AHE\sim \triangle ACH$ (g.g)
$\Rightarrow AE.AC=AH^2(**)$
Từ $(*); (**)\Rightarrow AB.AD=AE.AC$ (đpcm)
1 tháng 2
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔHBA
=>\(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)
=>\(BA^2=BH\cdot BC\)
b: Sửa đề: Đường trung tuyến CM của ΔABC cắt HD tại N
Ta có: HD\(\perp\)AC
AB\(\perp\)AC
Do đó: HD//AB
=>ND//AM và HN//MB
Xét ΔCAM có ND//AM
nên \(\dfrac{ND}{AM}=\dfrac{CN}{CM}\left(1\right)\)
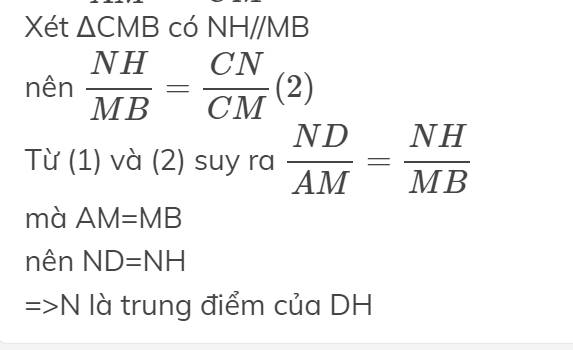
Xét ΔCMB có NH//MB
nên \(\dfrac{NH}{MB}=\dfrac{CN}{CM}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{ND}{AM}=\dfrac{NH}{MB}\)
mà AM=MB
nên ND=NH
=>N là trung điểm của DH
28 tháng 3 2023
a: Xét ΔAHB vuông tại H và ΔCAB vuông tại A có
góc B chung
=>ΔAHB đồng dạng với ΔCAB
b: \(BC=\sqrt{15^2+20^2}=25\left(cm\right)\)
HB=15^2/20=9cm
c: AD*AB=AH^2
AE*AC=AH^2
=>AD*AB=AE*AC
20 tháng 3 2022
Xét tam giác AEH và tam giác AHB, có:
\(\widehat{AHB}=\widehat{AEH}=90^0\)
\(\widehat{A}:chung\)
Vậy tam giác AEH đồng dạng tam giác AHB ( g.g )