Cho tam giác ABC vuông tại A , đường cao AH , HC - HB = AB . Cmr: BC= 2AB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cách 1 :
HC -HB = AB, HC +HB =BC
nhân 2 vế ta có HC^2 -HB^2 =AB.BC (1).
Áp dụng Pitago ta có HC ^2 =AC^2-AH^2, HB^2 = AB^2 -AH^2 nên HC^2 - HB^2 =AC^2 -AB^2 = (BC^2 -AB^2 ) -AB^2 = BC^2 -2AB^2 ,(2). Từ (1 ) và (2 ) có BC^2 - 2AB^2 =AB.BC
<=> BC^2 -AB.BC - 2AB^2 = 0
<=> (BC +AB) (BC -2AB ) = 0,
do AB +BC >0 => BC - 2AB = 0 => BC = 2AB
Cách 2:
Dựa vào đường xiên và hình chiếu :
lấy điểm D nằm giữa H,C sao cho HD = HB
==> AB = AD ( do có 2 hình chiếu bằnng nhau )
Đồng thời : AB = HC -- HB ( gt) = HC --HD = CD => AB = CD
nên : AD = CD
Kẻ đường cao DK xuống AC ==> AK = KC (do có 2 đxiên bằng nhau)
Nên K là trung điểm của AC và DK // AB ( do cùng vuông góc AC ) Từ đó D là trung điểm của BC ( đường trung bình )
==> BC = 2. BD = 2. CD , thay CD = AB ta được
----->BC = 2 .AB


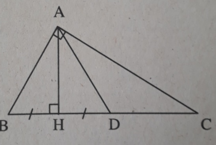
Trên HC lấy D sao cho HD = HB. Tam giác ABD có đường cao AH là trung tuyến nên là tam giác cân, suy ra
∠(ADB) = ∠B . (1)
Ta có: DC = HC – HD = HC – HB = AB = AD ( vì tam giác ABD cân tại A)
Nên ΔADC cân tại D, do đó ∠(DAC) = ∠C (2)
Ta có; ∠ADB + ∠DAC = ∠BAC = 90º (3)
Và ∠B + ∠C = 90º vì tam giác ABC vuông tại A (4)
Từ (2); (3) và (4) suy ra ∠(DAB) = ∠B . (5)
Từ (1) và (5) suy ra ∠(ADB) = ∠B = ∠(DAB) , do đó ΔABD là tam giác đều.
Suy ra AB = BD = AD = DC. Vậy BC = 2AB.

Do HC -HB = AB
Mà HC +HB =BC => nhân 2 vế ta có:
HC2 -HB2 =AB.BC (1).
Áp dụng định lí Pi-ta-go ta có:
HC2 =AC2-AH2
HB2 = AB2 -AH2
Nên HC2 - HB2 =AC2 -AB2 = (BC2 -AB2 ) -AB2 = BC2 -2AB2 ,(2).
Từ (1 ) và (2 ) có: BC2 - 2AB2 =AB.BC
<=> BC2 -AB.BC - 2AB2 = 0
<=> (BC +AB) (BC -2AB ) = 0,
Do AB +BC >0 nên BC = 2AB.
HC -HB = AB, HC +HB =BC
nhân 2 vế ta có HC^2 -HB^2 =AB.BC (1).
Áp dụng Pitago ta có HC ^2 =AC^2-AH^2, HB^2 = AB^2 -AH^2 nên HC^2 - HB^2 =AC^2 -AB^2 = (BC^2 -AB^2 ) -AB^2 = BC^2 -2AB^2 ,(2). Từ (1 ) và (2 ) có BC^2 - 2AB^2 =AB.BC
<=> BC^2 -AB.BC - 2AB^2 = 0
<=> (BC +AB) (BC -2AB ) = 0,
do AB +BC >0 => BC - 2AB = 0 => BC = 2AB.
:3



Bài 2:
Ta có: \(\dfrac{HB}{HC}=\dfrac{1}{3}\)
nên HC=3HB
Ta có: \(AH^2=HB\cdot HC\)
\(\Leftrightarrow HB^2=48\)
\(\Leftrightarrow HB=4\sqrt{3}\left(cm\right)\)
\(\Leftrightarrow BC=4\cdot HB=16\sqrt{3}\left(cm\right)\)
Bài 1:
ta có: \(AB=\dfrac{1}{2}AC\)
\(\Leftrightarrow\dfrac{HB}{HC}=\dfrac{1}{4}\)
\(\Leftrightarrow HC=4HB\)
Ta có: \(AH^2=HB\cdot HC\)
\(\Leftrightarrow HB=1\left(cm\right)\)
\(\Leftrightarrow HC=4\left(cm\right)\)
hay BC=5(cm)
Xét ΔBAC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AB^2=HB\cdot BC\\AC^2=HC\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=\sqrt{5}\left(cm\right)\\AC=2\sqrt{5}\left(cm\right)\end{matrix}\right.\)

Bài 2:
Xét ΔABC có
\(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{25}{13}\left(cm\right)\\CH=\dfrac{144}{13}\left(cm\right)\end{matrix}\right.\)
Bài 1:
Ta có: \(\dfrac{AB}{AC}=\dfrac{5}{6}\)
\(\Leftrightarrow HB=\dfrac{25}{36}HC\)
Ta có: \(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC^2\cdot\dfrac{25}{36}=900\)
\(\Leftrightarrow HC=36\left(cm\right)\)
hay HB=25(cm)