Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác góc B cắt AC tại D. Kẻ DH vuông góc với BC. Lấy điểm E trên cạnh AC sao cho AE = AB. Đường thẳng vuông góc với AE tại E cắt DH tại K. Qua B kẻ đường vuông góc với EK tại I. Chứng minh:
a, BA = BH (Đã chứng minh)
b, Góc DBK = 45 độ (Đã chứng minh)
c, BC = IK + AC
Mong được mọi người giúp đỡ! Em xin cảm ơn trước ạ!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 3 2021
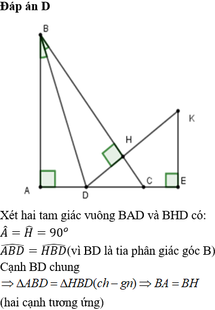
a) Xét ΔABD vuông tại A và ΔHBD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)(BD là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔABD=ΔHBD(cạnh huyền-góc nhọn)
Suy ra: BA=BH(hai cạnh tương ứng)
21 tháng 4 2021
a) Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)(BD là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔBAD=ΔBHD(cạnh huyền-góc nhọn)
Suy ra: BA=BH(Hai cạnh tương ứng)
12 tháng 2 2016
a ) xét 2 tam giác BAD và tam giác BHD (góc A= góc H= 90 độ)
ta có: cạnh huyền BD chung
góc ABD= góc HBD (vì BD là phân giác góc B)
=>tam giác BAD=tam giác BHD(cạnh huyền-góc nhọn)
<=>BA=BH (2 cạnh tương ứng)
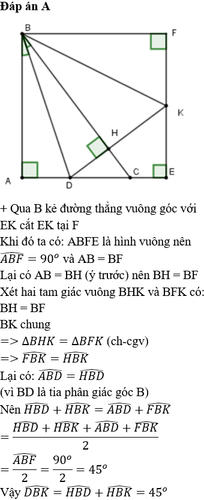
: -Kéo dài EK cắt đường thẳng vuông góc với AB kẻ từ B tại Q.
-Chứng minh được: AB=AE=BQ. Mà theo phần a), ta có: BA=BH => BH=BQ.
=> tam giác BHK= tam giác BQK( cạnh huyền- cạnh góc vuông).
=> góc HBK= góc QBK. Mà theo phần a), ta có: góc ABD= góc DBH.
=> góc DBK= 1/2.góc ABD. Mà góc ABD= 90 độ.
=> góc DBK=45 độ.(đpcm)
