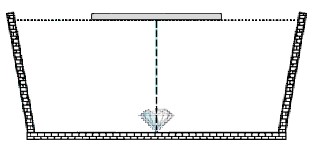
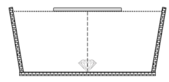
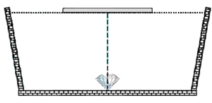
Một cái bể sâu 1,2m chứa đầy nước. Một tia sáng mặt trời rọi vào mặt nước dước góc tới i có \(\tan i=\frac{4}{3}\). Tính độ dài của quang phổ do tia sáng tạo ra ở đáy bể. Cho biết: chiết suất của nước đối với ánh sáng đỏ và ánh sáng tím lần lượt là \(n_đ=1,328\)và \(n_t=1,343\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
28 tháng 4 2018
Tia sáng Mặt Trời vào nước bị tán sắc và khúc xạ. Tia đỏ lệch ít nhất, tia tím lệch nhiều nhất.
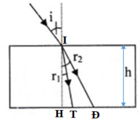
Ta có: tan i = 4/3 → i = 53,1o → sin i = 0,8
Áp dụng định luật khúc xạ tại I ta có: sin i = nđ. sin r2 = nt. sin r1
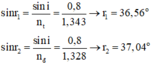
Xét tam giác vuông IHT, ta có: tan r1 = HT/IH ⇒ HT = h. tan r1
Xét tam giác vuông IHĐ, ta có: tan r2 = HĐ/IH ⇒ HĐ = h. tan r2
Độ dài quang phổ do tia sáng tạo ở đáy bể là :
ΔD = HĐ – HT = h.(tan r2 – tan r1) = 1,2.(tan 37,04o – tan 36,56o) = 0,01568m = 1,568cm
VT
2 tháng 1 2017
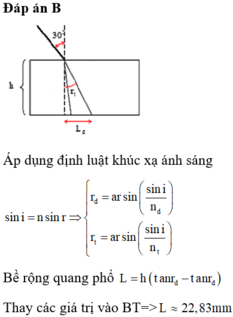
Đáp án B
sin r d = sin 30 o 1 , 328 ⇒ r d = 22 , 11742 o sin r t = sin 30 o 1 , 361 ⇒ r t = 21 , 553936 o
Bề rộng quang phổ ở đáy bể:
D = 2 tan 22 , 11742 o − tan 21 , 553936 o ≈ 0 , 02283 m = 22 , 83 m m
VT
22 tháng 6 2019
Chọn đáp án B
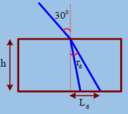
Áp dụng định luật khúc xạ ánh sáng : sini = nsinr → r d = a r sin sin i n d r t = a r sin sin i n t
Bề rộng quang phổ : L = h ( tan r d – tan r t )
→ Thay các giá trị vào biểu thức, ta thu được L ≈ 22 , 83 m m
VT
15 tháng 10 2019
Đáp án B
+ Áp dụng định luật khúc xạ ánh sáng
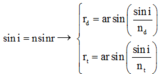
+ Bề rộng quang phổ : 
→ Thay các giá trị vào biểu thức, ta thu được L = 22,83 mm.
