Cho trước 5 điểm M; N; P; Q; R trong đó chỉ có 3 điểm P; Q; R thẳng hàng ngoài ra không còn 3 điểm nào thẳng hàng. Vẽ các đường thẳng đi qua các cặp điểm. Hỏi vẽ được bao nhiêu đường thẳng? Đó là những đường thẳng nào?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TK
ttanjjiro kamado
2 tháng 1 2022
Đúng(0)
Những câu hỏi liên quan
17 tháng 1
a: TH1: Chọn 1 điểm trong 2 điểm M,N; 1 điểm trong 3 điểm P,Q,R
Số cách chọn 1 điểm trong 2 điểm M,N là 2 cách
Số cách chọn 1 điểm trong 3 điểm P,Q,R là 3 cách
=>Có 2*3=6(cách)
TH2: Vẽ đường thẳng PQR
=>Có 1 cách
TH3: Vẽ đường thẳng MN
=>Có 1 cách
Tổng số đường thẳng là:
6+1+1=8(đường)
b: TH1: Chọn 1 điểm trong 5 điểm thẳng hàng, chọn 1 điểm trong 4 điểm không thẳng hàng
Số cách chọn 1 điểm trong 5 điểm thẳng hàng là 5 cách
Số cách chọn 1 điểm trong 4 điểm không thẳng hàng là 4 cách
=>Có 5*4=20 đường thẳng
TH2: Vẽ 1 đường thẳng đi qua 5 điểm thẳng hàng
=>Có 1 đường thẳng
TH3: Chọn 2 điểm trong 4 điểm không thẳng hàng
=>Có \(C^2_4=6\left(đường\right)\)
Số đường thẳng tất cả là:
20+1+6=27(đường)
11 tháng 9 2020
M chính là giao điểm của AB và Cd
Khi đó M,A,B thẳng hàng và M,C,D thẳng hàng
CM
11 tháng 1 2019
Quy tắc đặt tương ứng điểm M với điểm M’ nêu trên không phải là một phép biến hình vì M’không phải là điểm duy nhất được xác định trên mặt phẳng
Ví dụ minh họa: a = 4 cm
CM
1 tháng 11 2019
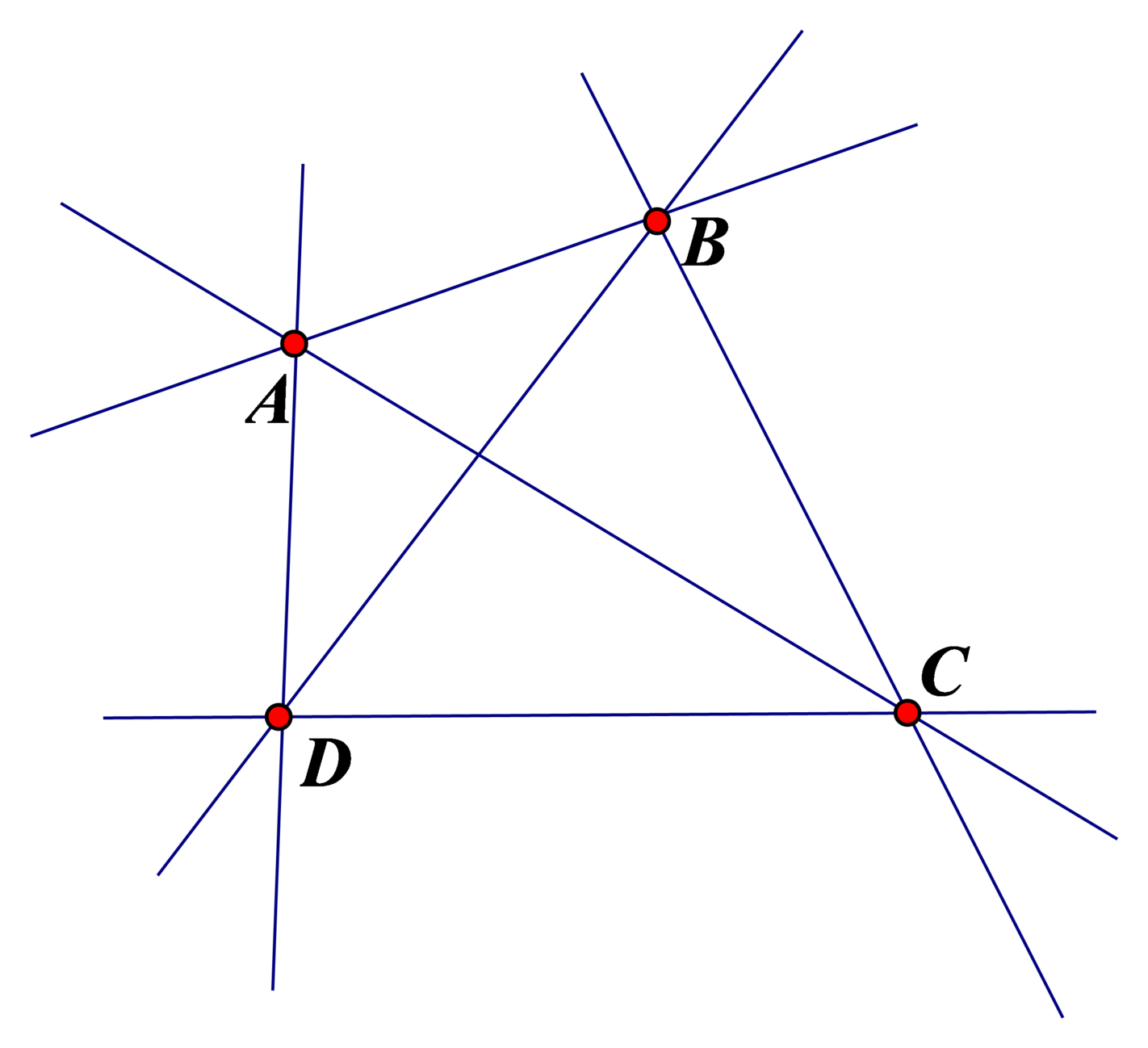
a) Với 4 điểm A, B, C, D cho trước trong đó không có ba điểm bất kì nào thẳng hàng thì có thể vẽ được 6 đường thẳng là: AB , AC , AD , BC , BD , CD .
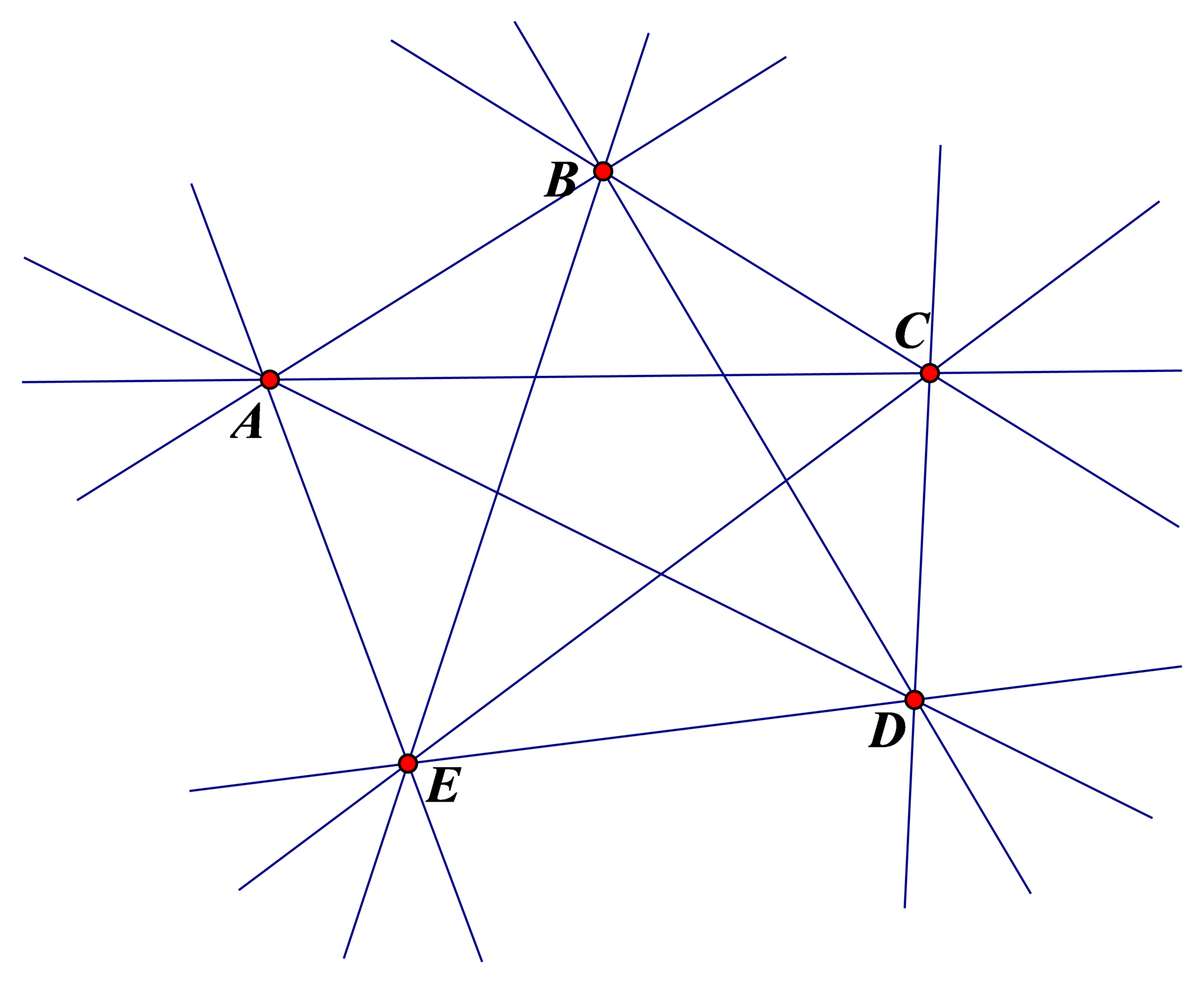
b) Với 5 điểm A, B, C, D, E cho trước trong đó không có ba điểm bất kì nào thẳng hàng thì có thể vẽ được 10 đường thẳng là: AB , AC , AD , AE , BC , BD , BE , CD , CE , DE .
c) Chọn một trong số n điểm đã cho rồi nối điểm đó với n-1 điểm còn lại ta được n-1 đường thẳng.
Làm như vậy với tất cả n điểm ta được n(n-1) đường thẳng. Nhưng mỗi đường thẳng được tính hai lần, do đó ta vẽ được n . n − 1 2 đường thẳng.
1 tháng 1 2023
Bài 2:
Xét tứ giác ABCD có
N là trung điểm chung của AC và BD
nên ABCD là hình bình hành
=>AD//BC và AD=BC
Xét tứ giác AEBC có
M là trung điểm chung của AB và EC
nên AEBC là hình bình hành
=>AE//BC và AE=BC
=>AD//AE và AD=AE
=>A là trung điểm của DE
28 tháng 8 2020
a,gọi I là trung điểm của AB, vì A và B là 2 điểm cố định => I cũng cố định
=> vt IA+vt IB=0
=>|vt MA+vtMB|=|vtMA-vtMB|
<=> |vtMI+vtIA+vtMI+vtIB|=|vtMI+vtMA-vtMI-vtIB|
<=>|2.vtMI|=|vtBA|
<=> 2,MI=BA
=> MI=BA/2
=> M thuộc (I;AB/2)