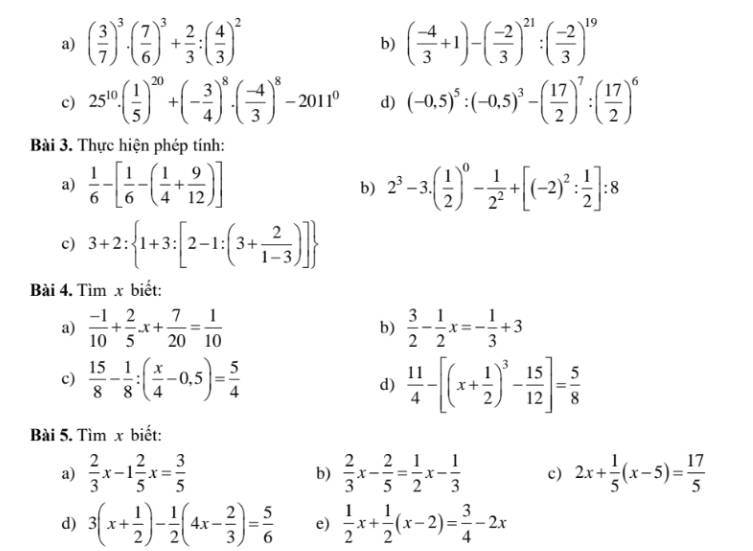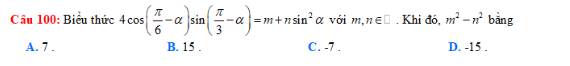giúp mik bài này với ạ, mik cần gấp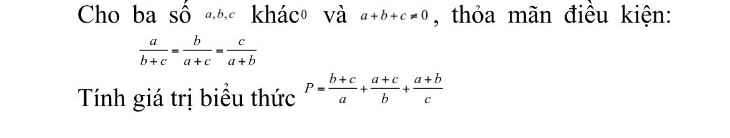 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 8 2023
4:
a: =>2/5x+7/20-2/20=1/10
=>2/5x+5/20=1/10
=>2/5x=1/10-1/4=4/40-10/40=-6/40=-3/20
=>x=-3/20:2/5=-3/20*5/2=-15/40=-3/8
b: 3/2-1/2x=-1/3+3=8/3
=>1/2x=3/2-8/3=9/6-16/6=-7/6
=>x=-7/6*2=-7/3
c: 15/8-1/8:(1/4x-0,5)=5/4
=>1/8:(1/4x-1/2)=15/8-5/4=15/8-10/8=5/8
=>1/4x-1/2=1/8:5/8=1/5
=>1/4x=1/5+1/2=7/10
=>x=7/10*4=28/10=2,8
d: \(\Leftrightarrow\left[\left(x+\dfrac{1}{2}\right)^3-\dfrac{5}{4}\right]=\dfrac{11}{4}-\dfrac{5}{8}=\dfrac{22-5}{8}=\dfrac{17}{8}\)
=>\(\left(x+\dfrac{1}{2}\right)^3=\dfrac{17}{8}+\dfrac{5}{4}=\dfrac{27}{8}\)
=>x+1/2=3/2
=>x=1
TM
0
KV
31 tháng 10 2023
Bài 1
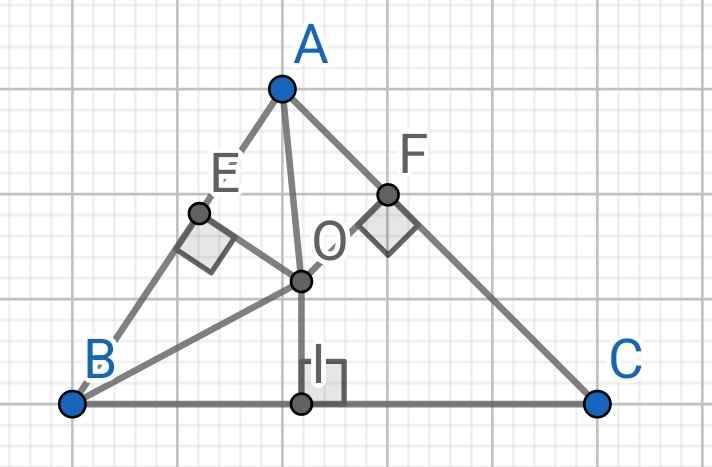Do BO là tia phân giác của ∠ABC (gt)
⇒ ∠OBE = ∠OBI
Do AO là tia phân giác của ∠BAC (gt)
⇒ ∠OAE = ∠OAF
Xét hai tam giác vuông: ∆OAE và ∆OAF có:
OA chung
∠OAE = ∠OAF (cmt)
⇒ ∆OAE = ∆OAF (cạnh huyền - góc nhọn)
⇒ OE = OF (hai cạnh tương ứng) (1)
Xét hai tam giác vuông: ∆OBE và ∆OBI có:
OB chung
∠OBE = ∠OBI (cmt)
⇒ ∆OBE = ∆OBI (cạnh huyền - góc nhọn)
⇒ OE = OI (hai cạnh tương ứng) (2)
Từ (1) và (2) ⇒ OE = OF = OI
KV
31 tháng 10 2023
Bài 2
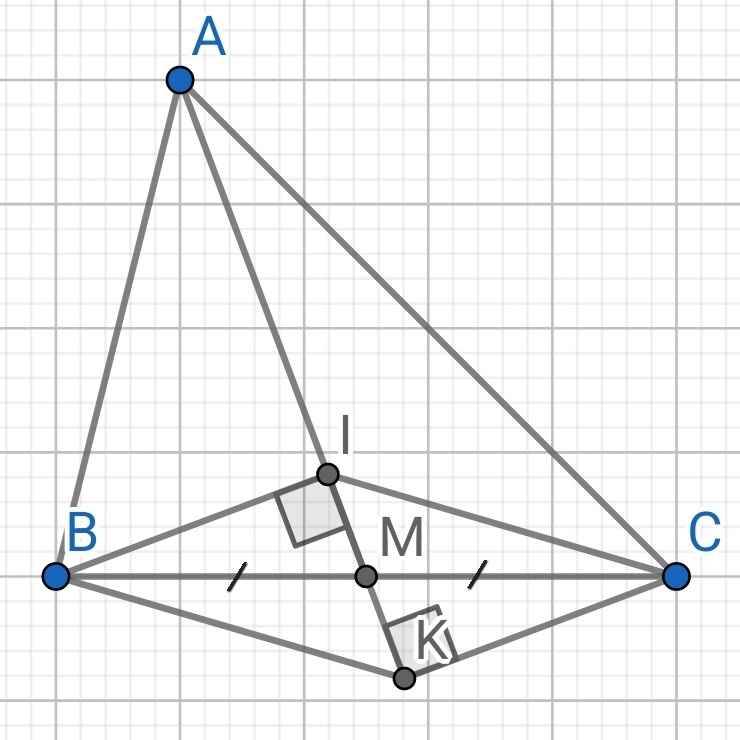a) Xét hai tam giác vuông: ∆BMI và ∆CMK có:
BM = CM (gt)
∠BMI = ∠CMK (đối đỉnh)
⇒ ∆BMI = ∆CMK (cạnh huyền - góc nhọn)
⇒ BI = CK (hai canhk tương ứn
b) Do ∆BMI = ∆CMK (cmt)
⇒ MI = MK (hai cạnh tương ứng)
Xét ∆BMK và ∆CMI có:
MK = MI (cmt)
∠BMK = ∠CMI (đối đỉnh)
BM = CM (gt)
⇒ ∆BMK = ∆CMI (c-g-c)
⇒ ∠MBK = ∠MCI (hai góc tương ứng)
Mà ∠MBK và ∠MCI là hai góc so le trong)
⇒ BK // CI
BN
1
14 tháng 3 2022
uses crt;
var st:string;
d,i,t,x,y,a,b:integer;
begin
clrscr;
readln(st);
d:=length(st);
for i:=1 to d do write(st[i]:4);
writeln;
t:=0;
for i:=1 to d do
begin
val(st[i],x,y);
t:=t+x;
end;
writeln(t);
val(st[d],a,b);
if (a mod 2=0) then write(1)
else write(-1);
readln;
end.
BN
1
13 tháng 3 2022
#include <bits/stdc++.h>
using namespace std;
long long a[1000],i,n,t,dem,t1;
int main()
{
cin>>n;
for (i=1; i<=n; i++) cin>>a[i];
t=0;
for (i=1; i<=n; i++) if (a[i]%2==0) t+=a[i];
cout<<t<<endl;
t1=0;
dem1=0;
for (i=1; i<=n; i++)
if (a[i]<0)
{
cout<<a[i]<<" ";
t1+=a[i];
dem1++;
}
cout<<endl;
cout<<fixed<<setprecision(1)<<(t1*1.0)/(dem1*1.0);
return 0;
}
BN
1
13 tháng 3 2022
#include <bits/stdc++.h>
using namespace std;
long long a,b;
//chuongtrinhcon
long long gcd(long long a,long long b)
{
if (b==0) return(a);
return gcd(b,a%b);
}
//chuongtrinhchinh
int main()
{
cin>>a>>b;
cout<<max(a,b)<<endl;
cout<<gcd(a,b)<<endl;
if ((a>0 && b>0) or (a<0 && b<0)) cout<<a/gcd(a,b)<<" "<<b/gcd(a,b);
else cout<<"-"<<-a/gcd(-a,b)<<" "<<b/gcd(-a,b);
return 0;
}
3 tháng 9 2021
b: Xét ΔABE vuông tại A có AH là đường cao ứng với cạnh huyền BE
nên \(BH\cdot BE=AB^2\left(1\right)\)
Xét ΔABC vuông tại B có BH là đường cao ứng với cạnh huyền AC
nên \(AH\cdot AC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BE=AH\cdot AC\)
BA
1
21 tháng 7 2023
4*cos(pi/6-a)*sin(pi/3-a)
=4*(cospi/6*cosa+sinpi/6*sina)*(sinpi/3*cosa-sina*cospi/3)
=4*(căn 3/2*cosa+1/2*sina)*(căn 3/2*cosa-1/2*sina)
=4*(3/4*cos^2a-1/4*sin^2a)
=3cos^2a-sin^2a
=3(1-sin^2a)-sin^2a
=3-4sin^2a
=>m=3; n=-4
m^2-n^2=-7