Giúp mình với: So sánh (2+1)(2^2+1)(2^3+1)...(2^512+1) với 2^1024
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt: \(A=1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+...+\dfrac{1}{512}+\dfrac{1}{1024}\)
\(\Rightarrow\dfrac{4}{2}A=\dfrac{4}{2}\left(1+\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{1024}\right)\)
\(\Rightarrow2A=2+1+\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{512}\)
\(\Rightarrow2A-A=\left(3+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+...+\dfrac{1}{512}\right)-\left(1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+...+\dfrac{1}{1024}\right)\)
\(\Rightarrow A=\left(\dfrac{1}{2}-\dfrac{1}{2}\right)+\left(\dfrac{1}{4}-\dfrac{1}{4}\right)+...+\left(3-1-\dfrac{1}{1024}\right)\)
\(\Rightarrow A=2-\dfrac{1}{1024}\)
\(\Rightarrow A=\dfrac{2047}{1024}\)
1+(1)/(2)+(1)/(4)+(1)/(8)+...+(1)/(512)+(1)/(1024)
A x 2 = 1 - ( 1/2 + 1/4 + 1/8 + 1/16 + ..... + 1/512 + 1/1024 ) - 1/1024
A x 2 = 1 - 1/1024 + A
A x 2 - A = 1 - 1/1024
A = 1 - 1/1024
A = 1023 /1024

A = 1/2 - 1/4 - 1/8 -...- 1/512 - 1/1024
2A = 2(1/2 - 1/4 - 1/8 -...- 1/512 - 1/1024)
2A = 1 - 1/2 - 1/8 -...- 1/1024 - 1/2048
2A - A = 1 - 1/2 - 1/8 -....- 1/1024 - 1/2048 - (1/2 - 1/4 - 1/8 - ...- 1/512 - 1/1024)
A = 1 - 1/2048
A = 2047/2048
Em mới học lớp 6, vậy anh thua em rồi. HIHI


Đặt A = 1 + 2 + 4 + 8 + 16 + ... + 1024
2A = 2 + 4 + 6 + 8 + 16 + 32 + ... + 2048
2A - A = ( 2 + 4 + 8 + 16 + 32 + ... + 2048 ) - ( 1 + 2 + 4 + 8 + 16 + ... + 1024 )
A = 2048 - 1
A = 2047


1/2=1/1-1/2
1/4=1/2-1/4
1/8=1/4-1/8
...................
1/1024=1/512-1/1024
Đặt biểu thức=A
A=1/1-1/2+1/2-1/4+1/4-1/8+........+1/512-1/1024
A=1/1-1/1024
A=1023/1024
bạn thấy cách của mik có dễ hiểu ko,nếu dễ hiểu thì k nha
có cách khác : 1/2+ 1/4= 3/4
1/2+ 1/4 +1/8 = 7/8
vậy :1/2+ 1/4 +1/8 + ....+ 1/1024 =1023/1024
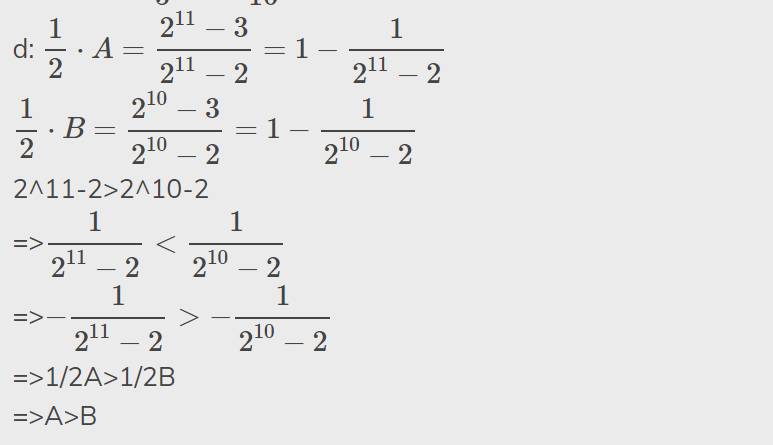
Bạn ghi sai đề rồi nhé!
Đặt \(A=\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)...\left(2^{512}+1\right)\) và \(B=2^{1024}\)
Khi đó, xét \(A=\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)...\left(2^{512}+1\right)\) và nhân hai vế của đẳng thức trên với \(\left(2-1\right)\), ta được:
\(A=\left(2-1\right)\left(2+1\right)\left(2^2+1\right)\left(2^4+1\right)...\left(2^{512}+1\right)\)
\(=\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)...\left(2^{512}+1\right)\)
\(=\left(2^4-1\right)\left(2^4+1\right)...\left(2^{512}+1\right)\)
\(=\left(2^8-1\right)...\left(2^{512}+1\right)\)
\(A=\left(2^{512}-1\right)\left(2^{512}+1\right)=2^{1024}-1\)
Vì \(2^{1024}-1<2^{1024}\) nên \(B>A\)