Cho tam giác ABC vuông tại A (AB < AC), vẽ đường cao AH. Trên đoạn thẳng BH lấy một điểm E , từ E hạ EM vuông góc với AB ( M thuộc AB ) và EN vuông góc với AC( N thuộc AC ).
a/ Chứng minh : AE = MN
b/ Gọi K là điểm đối xứng của điểm A qua N. Tứ giác MNKE là hình gì? Vì sao?
c/ Gọi O là giao điểm của MN và AE ; I là giao điểm của MK và EN. Chứng minh : IO //AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/
Ta có
\(\widehat{A}=90^o;\widehat{MHN}=90^o\) => A và H cùng nhìn MN dưới 1 góc vuông nên A; H thuộc đường tròn đường kính MN => A; M; H; N cùng thuộc 1 đường tròn
Xét tg vuông AHC có
\(MA=MC\Rightarrow HM=MA=MC=\dfrac{AC}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
=> tg AMH cân tại M \(\Rightarrow\widehat{MAH}=\widehat{MHA}\)
Mà
\(\widehat{NAH}+\widehat{MAH}=\widehat{A}=90^o\)
\(\widehat{NHA}+\widehat{MHA}=\widehat{MHN}=90^o\)
\(\Rightarrow\widehat{NAH}=\widehat{NHA}\) => tg NAH cân tại N => NA=HN (1)
Xét tg vuông ABH có
\(\widehat{NAH}+\widehat{B}=90^o\)
\(\widehat{NHA}+\widehat{NHB}=\widehat{AHB}=90^o\)
Mà \(\widehat{NAH}=\widehat{NHA}\) (cmt)
\(\Rightarrow\widehat{B}=\widehat{NHB}\) => tg BHN cân tại N => NB=HN (2)
Từ (1) và (2) => NA=NB => N là trung điểm AB
b/
Ta có
NA=NB (cmt); MA=MC (gt) => MN là đường trung bình của tg ABC
=> MN//BC
Gọi O là giao của MN với AH. Xét tg ABH có
MN//BC => NO//BH
NA=NB (cmt)
=> OA=OH (trong tg đường thẳng đi qua trung điểm 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại) => O à trung điểm AH
Ta có
\(HE\perp AB\left(gt\right);AC\perp AB\left(gt\right)\) => HE//AC => HE//AF
\(HF\perp AC\left(gt\right);AB\perp AC\left(gt\right)\) => HF//AB => HF//AN
=> AEHF là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Gọi O' là giao của EF với AH => O'A=O'H (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường) => O' là trung điểm của AH
Mà O cũng là trung điểm của AH (cmt)
=> \(O'\equiv O\) => AH; MN; EF cùng đi qua O

Bạn tự vẽ hình nhé!
a) Xét tam giác vuông ABH có: góc ABH + BAH = 90o
Lại có: góc EAM + BAH = 90o (do góc EAB = 90o)
=> góc ABH = EAM
Xét tam giác vuông ABH và EAM có: góc ABH = EAM ; cạnh AB = EA
=> tam giác vuông ABH = EAM (cạnh huyền - góc nhọn)
=> BH = AM ;AH = EM
Ta có HM = AM + AH = BH + EM
Tương tự, tam giác vuông ANF = CHA => AN = CH; NF = HA
Ta có: HN = HA + AN = NF + CH
b) Ta có: EM = NF ( = cùng = HA)
góc IEM = IFN (2 góc So le trong do FN // EM)
Mà góc FNI = IME (= 90o)
=> tam giác INF = IME ( g- c - g)
=> IN = IM => I là trung điểm của EF

a: Xét ΔADB và ΔADE có
AD chung
góc BAD=góc EAD
AB=AE
=>ΔABD=ΔAED
b: Xét ΔBHD vuông tại H và ΔEKD vuông tại K có
DB=DE
góc DBH=góc DEK
=>ΔBHD=ΔEKD
=>BH=EK
c: góc DEM=góc KDE
góc KDE=góc BDH
=>góc DEM=góc BDH
d: góc DEM+góc ACD
=góc BDH+góc ACD
=90 độ-góc CDE

a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AH^2=HB\cdot HC\left(1\right)\)
Xét ΔABH vuông tại H có HE là đường cao ứng với cạnh huyền AB
nên \(AH^2=AE\cdot AB\left(2\right)\)
Xét ΔACH vuông tại H có HF là đường cao ứng với cạnh huyền AC
nên \(AH^2=AF\cdot AC\left(3\right)\)
Từ (1), (2) và (3) suy ra \(AE\cdot AB=AF\cdot AC=BH\cdot HC\)
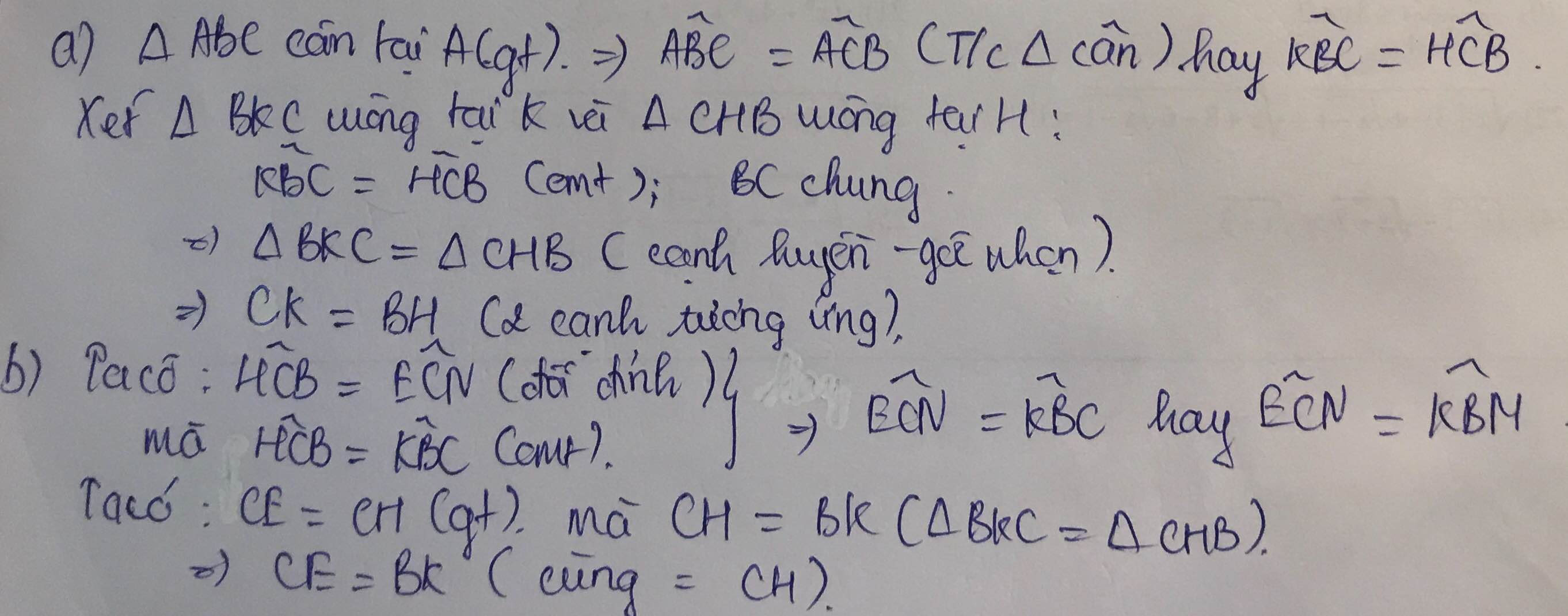

a: Xét tứ giác AMEN có
\(\widehat{AME}=\widehat{ANE}=\widehat{MAN}=90^0\)
Do đó: AMEN là hình chữ nhật
Suy ra: AE=NM