tìm các số tự nhiên xy biết (x,y)=1 và x+y/x2+y2 = 7/25
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
0
D
0
PT
22 tháng 4 2021
Bài 1: Ta có 200920 = (20092)10 = (2009.2009)10
2009200910 = (10001.2009)10
Mà 2009 < 10001 ➩ (2009.2009)10 < (10001.2009)10
Vậy 200920 < 2009200910
1 tháng 8 2023
10:
Vì n là số lẻ nên n=2k-1
Số số hạng là (2k-1-1):2+1=k(số)
Tổng là (2k-1+1)*k/2=2k*k/2=k^2 là số chính phương
11:
n^3-n^2+2n+7 chia hết cho n^2+1
=>n^3+n-n^2-1+n+8 chia hết cho n^2+1
=>n+8 chia hết cho n^2+1
=>n^2-64 chia hết cho n^2+1
=>n^2+1-65 chia hết cho n^2+1
=>n^2+1 thuộc {1;5;13;65}
=>\(n\in\left\{0;2;-2;2\sqrt{3};-2\sqrt{3};8;-8\right\}\)
19 tháng 8 2021
Bài 1:
a: Ta có: \(48751-\left(10425+y\right)=3828:12\)
\(\Leftrightarrow y+10425=48751-319=48432\)
hay y=38007
b: Ta có: \(\left(2367-y\right)-\left(2^{10}-7\right)=15^2-20\)
\(\Leftrightarrow2367-y=1222\)
hay y=1145
19 tháng 8 2021
Bài 2:
Ta có: \(8\cdot6+288:\left(x-3\right)^2=50\)
\(\Leftrightarrow288:\left(x-3\right)^2=2\)
\(\Leftrightarrow\left(x-3\right)^2=144\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=12\\x-3=-12\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=15\\x=-9\end{matrix}\right.\)
27 tháng 10 2021
Bài 11:
Ta có: \(n^3-n^2+2n+7⋮n^2+1\)
\(\Leftrightarrow n^3+n-n^2-1+n+8⋮n^2+1\)
\(\Leftrightarrow n^2-64⋮n^2+1\)
\(\Leftrightarrow n^2+1\in\left\{1;5;13;65\right\}\)
\(\Leftrightarrow n^2\in\left\{0;4;64\right\}\)
hay \(n\in\left\{0;-2;2;8;-8\right\}\)
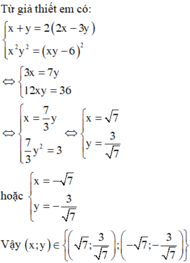
Ta có:(x,y) = 1 =>x, y nguyên tố cùng nhau
x
1
3
y
6
4
(LOẠI) (NHÂN)
Vậy x = 3;y = 4
Ta có:(x,y) = 1 =>x, y nguyên tố cùng nhau
X
1
3
Y
6
4
(LOẠI) (NHÂN)
Vậy x = 3;y = 4