Cho tam giác ABC nội tiếp đường tròn tâm O. Đường cao BD, CE cắt nhau ở H. BD, CE kéo dài lần lượt cắt đường tròn tại I,K. CMR:
a) A,D,H,E cùng thuộc 1 đường tròn
b) tam giác AIH, AKI cân
c) AO \(\bot\)DE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi G là trung điểm của BC
Ta có: ΔDBC vuông tại D(BD\(\perp\)AC tại D)
mà DG là đường trung tuyến ứng với cạnh huyền BC(G là trung điểm của BC)
nên \(DG=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)(1)
Ta có: ΔEBC vuông tại E(CE\(\perp\)AB)
mà EG là đường trung tuyến ứng với cạnh huyền BC(G là trung điểm của BC)
nên \(EG=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)(2)
Ta có: G là trung điểm của BC(gt)
nên \(BG=CG=\dfrac{BC}{2}\)(3)
Từ (1), (2) và (3) suy ra GB=GC=GE=GD
hay B,C,D,E cùng nằm trên một đường tròn(đpcm)

a) Ta có: \(\angle AEH+\angle ADH=90+90=180\Rightarrow AEHD\) nội tiếp (1)
Vì AK là đường kính \(\Rightarrow\angle ANK=90\)
\(\Rightarrow\angle ANH+\angle ADH=90+90=180\Rightarrow ANHD\) nội tiếp (2)
Từ (1) và (2) \(\Rightarrow A,N,E,H,D\) cùng thuộc 1 đường tròn
b) Ta có: \(\angle BEC=\angle BDC=90\Rightarrow BCDE\) nội tiếp
\(\Rightarrow\angle ADE=\angle ABC\)
Ta có: \(\angle OAC=\dfrac{180-\angle AOC}{2}=90-\dfrac{1}{2}\angle AOC=90-\angle ABC\)
\(\Rightarrow\angle ADE+\angle OAC=90\Rightarrow AO\bot DE\)
c) DE cắt BC tại Q'.Q'A cắt (O) tại N'
Xét \(\Delta Q'EB\) và \(\Delta Q'CD:\) Ta có: \(\left\{{}\begin{matrix}\angle Q'EB=\angle Q'CD\\\angle CQ'Dchung\end{matrix}\right.\)
\(\Rightarrow\Delta Q'EB\sim\Delta Q'CD\left(g-g\right)\Rightarrow\dfrac{Q'E}{Q'C}=\dfrac{Q'B}{Q'D}\Rightarrow Q'B.Q'C=Q'D.Q'E\)
Xét \(\Delta Q'N'B\) và \(\Delta Q'CA:\) Ta có: \(\left\{{}\begin{matrix}\angle Q'N'B=\angle Q'CA\\\angle CQ'Achung\end{matrix}\right.\)
\(\Rightarrow\Delta Q'N'B\sim\Delta Q'CA\left(g-g\right)\Rightarrow\dfrac{Q'N'}{Q'C}=\dfrac{Q'B}{Q'A}\Rightarrow Q'B.Q'C=Q'N'.Q'A\)
\(\Rightarrow Q'N'.Q'A=Q'D.Q'E\Rightarrow AN'DE\) nội tiếp
mà AEHD nội tiếp \(\Rightarrow A,N',D,E,H\) cùng thuộc 1 đường tròn
\(\Rightarrow N\equiv N'\Rightarrow Q\equiv Q'\Rightarrow\) đpcm

Chọn đáp án D.
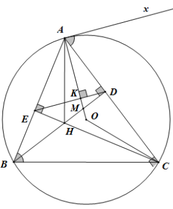
* Chứng minh tứ giác ADHE nội tiếp trong một đường tròn.

Trong nửa mặt phẳng bờ AC không chứa điểm B, vẽ tia tiếp tuyến Ax với đường tròn (O)


a, tính chất 3 đường cao trong tam giác nha bn.
b,2 góc vg cùng nhìn xuống cung BC =90 độ
c, chép nhầm đề oy bn phải là BHCK là hình bình hành mới đúng.
tam giác AKC nt đg trogn có ak là đg kính suy ra góc ACK =90 độ mà ADB= 90 SUY ra bd // kc hay BH //KC (1)
Tương tự trong tam giác AKB ta cm đc hc //kb (2)
từ (1) và (2) suy ra tứ giác đó là hbh
d,vì 4 điểm B,C,D,E cùng thược 1 đg tròn suy ra góc AED =ACB cùng bù với góc DEB xét 2 tam giác đó có góc a chung và góc AED =ACB suy ra đồng dạng trg hợp g -g

a: Xét tứ giác BCDE có
\(\widehat{BEC}=\widehat{BDC}=90^0\)
nên BCDE là tứ giác nội tiếp
hay B,C,D,E cùng thuộc một đường tròn