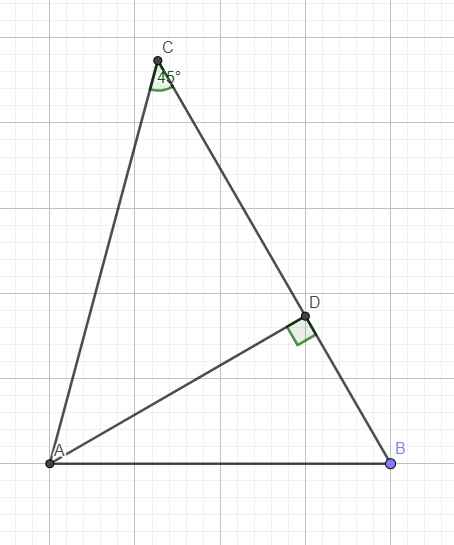
Cho tam giác ABC có góc B=45 độ,Ab=\(\sqrt{8}\) ,AC=\(\sqrt{13}\)Tính BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{AB}{AC}=\dfrac{\sqrt{6}}{3}\Rightarrow AB=\dfrac{AC\sqrt{6}}{3}\)
\(AB.AC=32\sqrt{6}\Rightarrow\dfrac{AC^2\sqrt{6}}{3}=32\sqrt{6}\)
\(\Rightarrow AC^2=96\Rightarrow AC=4\sqrt{6}\)
\(\Rightarrow AB=\dfrac{AC\sqrt{6}}{3}=8\)
Kẻ đường cao AD ứng với BC
Do \(C=45^0\Rightarrow\widehat{CAD}=90^0-45^0=45^0\Rightarrow\Delta ACD\) vuông cân tại D
\(\Rightarrow AD=CD=\dfrac{AC}{\sqrt{2}}=4\sqrt{3}\)
Pitago tam giác vuông ABD:
\(BD=\sqrt{AB^2-AD^2}=4\)
\(\Rightarrow BC=CD+BD=4+4\sqrt{3}\)
\(cosB=\dfrac{BD}{AB}=\dfrac{4}{8}=\dfrac{1}{2}\Rightarrow B=60^0\)
\(S_{ABC}=\dfrac{1}{2}AD.BC=\dfrac{1}{2}.4\sqrt{3}.\left(4+4\sqrt{3}\right)=...\)

Xét tam giác ABC
Theo định lí cos
\(AC^2=AB^2+BC^2-2AB.BCcos45=25\Rightarrow AC=5cm\)
Chu vi tam giác ABC là
AC + AB + BC = 7 + 3\(\sqrt{3}\)+5 = 12 + 3\(\sqrt{3}\)cm

a) Ta có:
\(\widehat{A}=180^o-60^o-45^o=75^o\)
Áp dụng định lý sin ta có:
\(\dfrac{BC}{sinA}=\dfrac{AC}{sinB}\)
\(\Rightarrow AC=\dfrac{BC\cdot sinB}{sinA}\)
\(\Rightarrow AC=\dfrac{a\cdot sin60^o}{sin75^o}=a\cdot\dfrac{3\sqrt{2}-\sqrt{6}}{2}\)
\(\dfrac{BC}{sinA}=\dfrac{AB}{sinC}\)
\(\Rightarrow AB=\dfrac{BC\cdot sinC}{sinA}\)
\(\Rightarrow AB=\dfrac{a\cdot sin45^o}{sin75^o}=a\cdot\left(\sqrt{3}-1\right)\)
b) \(cos75^o\)
\(=cos\left(30^o+45^o\right)\)
\(=cos30^o\cdot cos45^o-sin30^o\cdot sin45^o\)
\(=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{2}-\dfrac{1}{2}\cdot\dfrac{\sqrt{2}}{2}\)
\(=\dfrac{\sqrt{2}}{2}\cdot\left(\dfrac{\sqrt{3}-1}{2}\right)\)
\(=\dfrac{\sqrt{6}-\sqrt{2}}{4}\left(dpcm\right)\)

Đặt AB = c ; AC = b ; BC = a .
Ta có : \(b+c=13\) ; \(r=\dfrac{S}{p}=\sqrt{3}\) ( p \(=\dfrac{a+b+c}{2}\) )
Có : \(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\) nên : \(r=\sqrt{\dfrac{\left(p-a\right)\left(p-b\right)\left(p-c\right)}{p}}=\sqrt{3}\)
\(\Rightarrow\left(p-a\right)\left(p-b\right)\left(p-c\right)=3p\)
\(\Leftrightarrow\left(\dfrac{-a+b+c}{2}\right)\left(\dfrac{-b+a+c}{2}\right)\left(\dfrac{-c+a+b}{2}\right)=\dfrac{3\left(a+b+c\right)}{2}\)
\(\Leftrightarrow\left(-a+b+c\right)\left(-b+a+c\right)\left(-c+a+b\right)=12\left(a+b+c\right)\)
\(\Leftrightarrow\left(-a+13\right)\left(-b+a+c\right)\left(-c+a+b\right)=12\left(13+a\right)\)
\(\Leftrightarrow\left(-a+13\right)\left[a^2-\left(b-c\right)^2\right]=12\left(13+a\right)\) (2)
Có : \(\dfrac{b^2+c^2-a^2}{2bc}=cosA=cos60^o=\dfrac{1}{2}\) \(\Rightarrow b^2+c^2-a^2=bc\) \(\Leftrightarrow a^2=b^2+c^2-bc\) (1)
Mặt khác : \(b+c=13\Leftrightarrow b^2+c^2-bc+3bc=169\Leftrightarrow a^2=169-3bc\)
Từ (1) ; (2) suy ra : \(\left(-a+13\right)bc=12\left(13+a\right)\)
\(\Leftrightarrow\left(-a+13\right)\left(169-a^2\right)=36\left(13+a\right)\)
\(\Leftrightarrow\left(13-a\right)^2\left(13+a\right)=36\left(13+a\right)\)
\(\Leftrightarrow\left(13-a\right)^2=36\) \(\Leftrightarrow\left[{}\begin{matrix}13-a=6\\13-a=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=7\\a=19>13=b+c\left(L\right)\end{matrix}\right.\)
Vậy ...