Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gửi bạn lời giải. Có gì sai sót thì bạn góp ý nhé!
Kẻ \(\)$\(CH \perp AB\)$ tại H, $\(DK \perp AB\)$ tại K.
Áp dụng định lí Pytago vào tam giác ABC vuông tại C, ta có:
$\(AC^2=AB^2-BC^2=26^2-10^2=576\)$
Áp dụng hệ thức lượng vào tam giác ABC vuông tại C với đường cao CH, ta có:
$\(\dfrac{1}{CH^2}=\dfrac{1}{DK^2}=\dfrac{1}{AC^2}+\dfrac{1}{BC^2}=\dfrac{1}{100}+\dfrac{1}{576}=\dfrac{169}{14400}\)$ (do ABCD là hình thang cân)
⇒ $\(CH^2=DK^2=\dfrac{14400}{169}\)$
⇒ $\(CH=DK=\dfrac{120}{13}\)$
Áp dụng định lí Pytago vào tam giác CHB vuông tại H và tam giác AKD vuông tại K có:
$\(BH^2=AK^2=10^2-\dfrac{14400}{169}=\dfrac{2500}{169}\)$ ⇒ $\(BH=AK=\dfrac{50}{13}cm\)$ Ta có: $\(AB=AK+HK+BH=AK+CD+HK\)$ ⇒ $\(CD=AB-AK-HK=26-\dfrac{100}{13}=\dfrac{238}{13}\)$
Ta có: $\({S}_{ABCD}=\dfrac{(AB+CD).AH}{2}=\dfrac{(26+\dfrac{238}{13}).\dfrac{120}{13}}{2}=\dfrac{34560}{169} cm^2\)$

a) DDBC vuông có B C D ^ = 2 B D C ^ nên A D C ^ = B C D ^ = 60 0 và D A B ^ = C B A ^ = 120 0
b) Tính được DC = 2.BC = 12cm, suy ra PABCD = 30cm.
Hạ đường cao BK, ta có BK = 3 3 c m .
Vậy SABCD = 27 3 c m 2

Lời giải:
a) Vì $ABCD$ là hình thang cân nên $\widehat{D}=\widehat{C}$ và $AD=BC$
$\Rightarrow \frac{AD}{BC}=1$
Xét tam giác $ADE và $BCF$ có:
$\widehat{D}=\widehat{C}$ (cmt)
$\widehat{E}=\widehat{F}=90^0$
$\Rightarrow \triangle ADE\sim \triangle BCF$ (g.g)
$\Rightarrow \frac{DE}{CF}=\frac{AD}{BC}=1$
$\Rightarrow DE=CF$ (đpcm)
b) Vì $AB\parallel EF, EF\perp AE$ nên $AB\perp AE\Rightarrow \widehat{EAB}=90^0$
Tứ giác $ABFE$ có $\widehat{E}=\widehat{F}=\widehat{A}=90^0$ nên $ABFE$ là hình chữ nhật (đpcm)

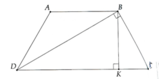
Kẻ CH,DK lần lượt vuông góc AB
ΔCAB vuông tại C
=>CA^2+CB^2=AB^2
=>CA^2+10^2=26^2
=>CA=24cm
ΔCAB vuông tại C có CH là đường cao
nên CH*AB=CA*CB
=>CH*26=10*24=240
=>CH=120/13(cm)
ΔCHB vuông tại H
=>HB^2+CH^2=CB^2
=>HB^2=10^2-(120/13)^2=2500/169(cm)
=>HB=50/13(cm)
Xét ΔDKA vuông tại K và ΔCHB vuông tại H có
DA=CB
góc DAK=góc CBH
=>ΔDKA=ΔCHB
=>KA=HB=50/13cm
KH=AB-AK-HB
=26-50/13*2=238/13(cm)
Xét tứ giác KDCH có
DC//KH
DK//CH
Do đó: KDCH là hình bình hành
=>DC=KH=238/13(cm)
S ABCD=1/2*(DC+AB)*CH
=1/2(238/13+26)*120/13
=34560/169(cm2)

Kẻ CH,DK vuông góc với AB
ΔCAB vuông tại C
=>CA^2+CB^2=AB^2
=>CA^2=26^2-10^2=576
=>CA=24(cm)
Xét ΔCAB vuông tại C có CH là đường cao
nên CH*AB=CA*CB
=>CH*26=24*10=240
=>CH=120/13(cm)
ΔCAB vuông tại C có CH là đường cao
nên BH*BA=CB^2
=>BH=10^2/26=100/26=50/13(cm)
Xét ΔDKA vuông tại K và ΔCHB vuông tại H có
DA=CB
góc DAK=góc CBH
=>ΔDKA=ΔCHB
=>BH=KA=50/13(cm)
=>KH=26-50/13*2=238/13(cm)
Xét tứ giác DCHK có
DC//HK
DK//HC
=>DCHK là hình bình hành
=>DC=HK=238/13(cm)
S ABCD=1/2(DC+AB)*CH
=1/2(238/13+26)*120/13
=60/13*576/13
=34560/169cm2
