cho tứ diện ABCD, có tam giác ABC vuông tại B, SA vuông góc với mặp phẳng (ABC). M là chân đường vuông góc hạ từ A đến SB. Trên SC lấy điểm N sao cho SM/SB=SN/SC. CMR:
a) BC vuông góc với (SAB)
b) AM vuông góc với (SBC)
c) AN vuông góc với SB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 5 2020
Trong mặt phẳng (SBC), nối HM kéo dài cắt BC tại K \(\Rightarrow AK\in\left(ABC\right)\)
Từ câu a có \(AM\perp\left(SBC\right)\) \(\Rightarrow AM\perp SC\)
Mà \(SC\perp AH\Rightarrow SC\perp\left(AHM\right)\Rightarrow SC\perp AK\) (1)
\(SA\perp\left(ABC\right)\Rightarrow SA\perp AK\) (2)
(1);(2) \(\Rightarrow AK\perp\left(SAC\right)\Rightarrow AK\perp AC\)
CM
5 tháng 1 2018
Chọn B.
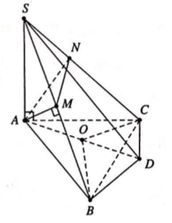
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, và D là điểm đối xứng với A qua O.
Ta có BD ⊥ AB (góc nội tiếp chắn nửa đường tròn).
Và BD ⊥ SA ⇒ BD ⊥ ( SAB ) ⇒ BD ⊥ AM .
Mặt khác AM ⊥ SB ⇒ AM ⊥ ( SBD ) ⇒ SD ⊥ AM .
Chứng minh tương tự ta được SD ⊥ AN ⇒ SD ⊥ ( AMN ) .
Ta có SD ⊥ ( AMN ) SA ⊥ ( ABC ) ⇒ ( ( AMN ) ; ( ABC ) ^ )
= ( SA ; SD ^ ) = ASD ^ .
Ta có: AD = 2 R ABC = BC sin A ^ = a 2
Vậy ( ( AMN ) ; ( ABC ) ^ ) = ASD ^ = arctan 1 = 45 o
