Cho a, b, c thuộc R và a, b, c khác 0 thỏa mãn b2 = a.c.Chứng minh a/c = ( a + 2015.b )2/ ( b + 2015.c )2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 8 2017
Sửa lại đề \(CM\)\(\frac{a}{c}=\frac{\left(a+20112b\right)^2}{\left(b+2012c\right)^2}\)
Có \(a,b,c\in R;a,b,c\ne0\)và \(b^2=ac\)
Ta có \(b^2=ac\Rightarrow\frac{a}{b}=\frac{b}{c}\)
Lại có \(\frac{a}{b}=\frac{b}{c}=\frac{2012b}{2012c}\Rightarrow\frac{a}{b}=\frac{a+2012b}{b+2012c}\)
\(\Rightarrow\frac{a^2}{b^2}=\frac{\left(a+2012b\right)^2}{\left(b+2012c\right)^2}\Rightarrow\frac{a^2}{ac}=\frac{\left(a+2012b\right)^2}{\left(b+2012c\right)^2}\)
Hay \(\frac{a}{c}=\frac{\left(a+2012b\right)^2}{\left(b+2012c\right)^2}\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
3 tháng 8 2017
\(\frac{\left(a+2012.b\right)^2}{\left(b+2012.c\right)^2}=\frac{a^2+2.2012.a.b+2012^2.b^2}{b^2+2.2012.b.c+2012^2.c^2}=\frac{a^2+2.2012.a.b+2012^2.a.c}{a.c+2.2012.b.c+2012^2.c^2}=\)
\(=\frac{a\left(a+2.2012.b+2012^2.c\right)}{c\left(a+2.2012.b+2012^2.c\right)}=\frac{a}{c}\)
Xem lại đề bài
CB
0
7 tháng 9 2023
Vì \(b^2=ac\) ta suy ra \(\dfrac{a}{b}=\dfrac{b}{c}\). Đặt \(a=kb\) và \(b=kc\).
Khi đó \(\dfrac{a}{c}=\dfrac{k\left(kc\right)}{c}=k^2\). (1)
Từ tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{2012b}{2012c}=\dfrac{a+2012b}{b+2012c}=k\), suy ra \(k^2=\dfrac{\left(a+2012b\right)^2}{\left(b+2012c\right)^2}\). (2)
Từ (1) và (2) suy ra \(k^2=\dfrac{a}{c}=\dfrac{\left(a+2012b\right)^2}{\left(b+2012c\right)^2}\) (đpcm)
PN
0
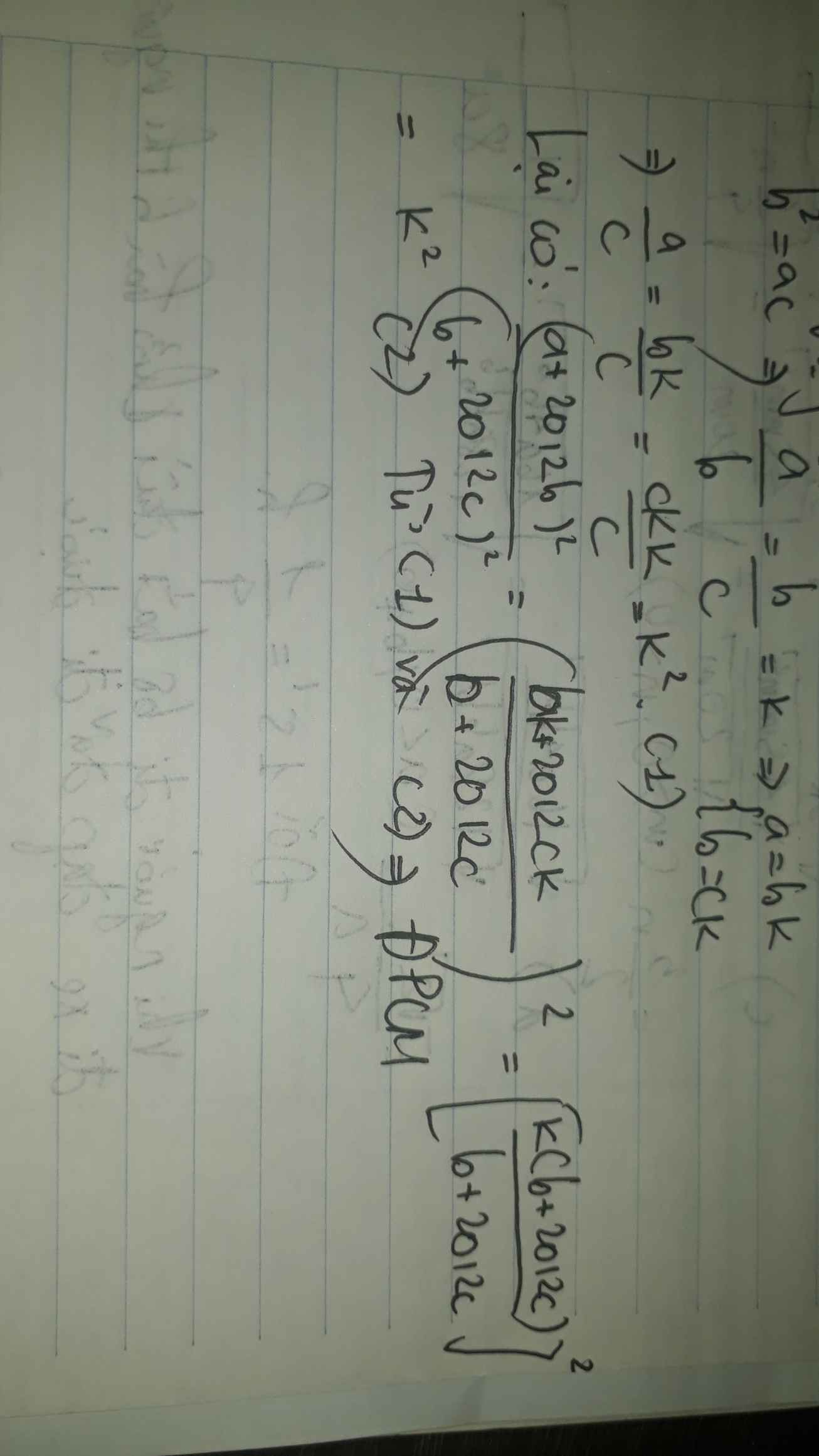
vì b2 = a.c nên \(\frac{a}{b}=\frac{b}{c}\Rightarrow\frac{a}{b}=\frac{2015.b}{2015.c}=\frac{a+2015.b}{b+2015.c}\)
\(\Rightarrow\left(\frac{a+2015.b}{b+2015.c}\right)^2=\left(\frac{a}{b}\right)^2=\frac{a^2}{b^2}=\frac{a^2}{a.c}=\frac{a}{c}\)
gần giống bài của mình