Hãy đặt 8 quân Hậu vào bàn cờ vua tiêu chuẩn sao cho không có quân Hậu nào tấn công được nhau. (màu của quân Hậu không có ý nghĩa trong trường hợp này)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 12 2021
Dưạ vào dạng này
Bài toán tám quân hậu là bài toán đặt tám quân hậu trên bàn cờ vua kích thước 8×8 sao cho không có quân hậu nào có thể "ăn" được quân hậu khác, hay nói khác đi không quân hậu nào có để di chuyển theo quy tắc cờ vua. Màu của các quân hậu không có ý nghĩa trong bài toán này. Như vậy, lời giải của bài toán là một cách xếp tám quân hậu trên bàn cờ sao cho không có hai quân nào đứng trên cùng hàng, hoặc cùng cột hoặc cùng đường chéo. Bài toán tám quân hậu có thể tổng quát hóa thành bài toán đặt n quân hậu trên bàn cờ n×n(n ≥ 4).
7 tháng 12 2021
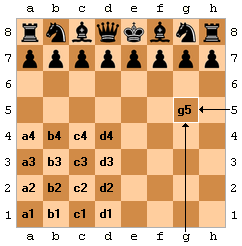
Theo hình ta thấy quãng đường quân hậu di chuyển là 1 tam giác vuông cân có cạnh góc vuông là cạnh chung với cạnh của bàn cờ
Ta có cạnh bàn cờ là \(\sqrt{40}=2\sqrt{10}\left(cm\right)\)
Áp dụng PTG, cạnh huyền của tam giác vuông cân là \(\sqrt{\left(2\sqrt{10}\right)^2+\left(2\sqrt{10}\right)^2}=4\sqrt{10}\left(cm\right)\)
Vậy tổng quãng đường quân hậu di chuyển là \(2\sqrt{10}\cdot2+4\sqrt{10}=8\sqrt{10}\left(cm\right)\)
HQ
Hà Quang Minh
Giáo viên
11 tháng 9 2023
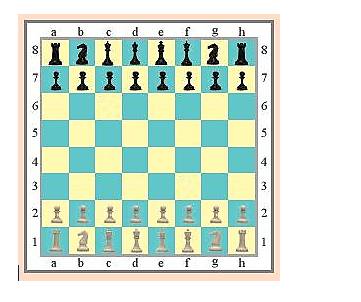
Quan sát bàn cờ ta thấy
- Quân Hậu Trắng đang ở giao của hàng 1 và cột d.
- Tại giao của cột b và hàng 8 là quân Mã đen.
7 tháng 12 2021
Một bàn cờ vua tiêu chuẩn sẽ có 8*8=64 ô.
Trừ ô quân Mã đứng, còn lại 63 ô.
Như vậy vì quân Mã di chuyển qua tất cả các ô, mỗi ô chỉ được đi qua 1 lần nên quân Mã sẽ phải thực hiện 63 nước đi.
Đặc điểm của quân Mã là nếu đi số nước lẻ thì nó sẽ dừng lại ở ô khác màu với ô nó đứng ban đầu, mà 63 là số lẻ do đó nơi nó kết thúc trong hành trình này sẽ là một ô khác màu với ô ban đầu nó đứng.
Nhưng góc đối diện với ô quân Mã đứng lúc đầu lại là ô cùng màu (vì nằm trên cùng đường chéo) nên việc quân Mã kết thúc tại góc đối diện theo đề bài sẽ không bao giờ có thể xảy ra.
Vậy không thể di chuyển Mã như đề bài yêu cầu.
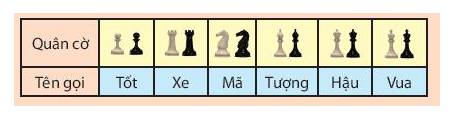
Tham khảo: Bài toán tám quân hậu – Wikipedia tiếng Việt